The Fröhlich charge transfer mode was initially erroneously proposed as an explanation for superconductivity. It turned out later that the described collective conductivity mechanism is indeed realized in quasi-one-dimensional conductors with charge density waves (CDWs), but the CDW conductivity is finite. Moreover, in the limit of a strong electric field E, the CDW conductivity, $\sigma_{\rm CDW}(\it E)$, approaches the conductivity of the electrons condensed in it in the normal (metallic) state, but never exceeds it. No universal explanation for this regularity has been proposed by now.

In this work, this regularity is probed on the NbS₃ monoclinic phase. NbS₃ compound is unique in that three CDWs are formed in it, and all three can slide in the presence of  electric field. The authors have suggested a way of mobility estimation, applicable both to the CDWs and to the quasiparticles forming them. It turned out that the difference between the mobilities of different CDWs reaches almost two orders of magnitude. At the same time, the mobility of each of them is close to the normal-state mobility of the quasiparticles forming it. Moreover, there is a correlation between the temperature dependences of CDW and quasiparticle mobilities. For example, both the CDW-0 state and its constituent quasiparticles exhibit a dielectric behavior. In this case, the mobility value, 0.04–0.05 cm²/Vs, evidences for the hopping origin of conduction. The results of the work actualize questions about the mechanism of limiting conductivity of charge density waves.

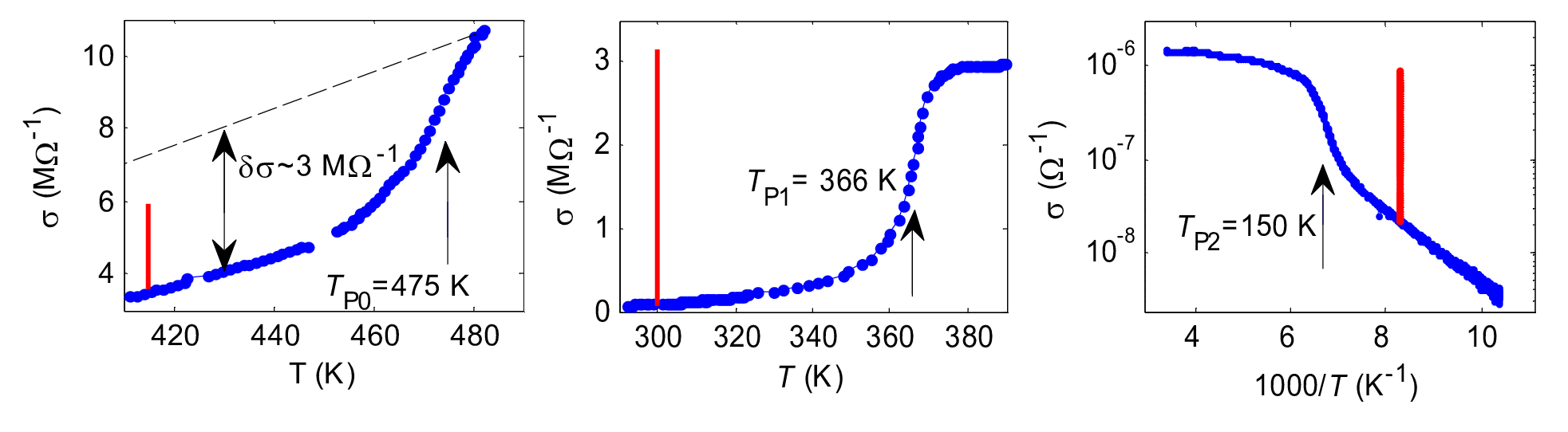
Fragments of temperature dependences of conductivity of NbS₃ samples in the regions of the three CDW transitions: T_P0 (left), T_P1 (middle) and T_P2 (right). The vertical red lines show the “projections” of the $\sigma (\it E)$ dependences measured up to the high fields. The lines are placed at the temperatures, at which $\sigma (\it E)$ was measured. The length of each line gives the estimate of $\sigma_{\rm CDW}(\infty)$. One can see that this value is comparable with the value of s step, $\delta \sigma$, at the corresponding CDW transition (the left panel illustrates the method of $\delta \sigma$ estimation).

S. Zybtsev, V.Ya. Pokrovskii, S. Nikonov, A. Mayzlakh, S. Zaitsev-Zotov 
JETP Letters 117, issue 2 (2023)