Fractional quantum Hall effect states at total Landau level filling factors $\nu=\nu_{\rm Q}=8/3$, 7/3, 4/3, and 5/4 were investigated in a bilayer electron system created in a wide (60 nm) GaAs quantum well placed between two field electrodes (gates). It was found that these fractional states appear or greatly enhance when a magnetic field is tilted from the normal to the plane of the electron system and integer quantum Hall effect states at $\nu=\nu_{\rm Q}=1$ and 2 become essentially weaker or even disappear. Using a new experimental technique consisting of simultaneous measurements of the magnetoresistance and Hall resistance, as well as two capacitances between the gates and the electron system [1, 2], we have established that these fractions arise under conditions when an incompressible state is realized in the layer with a higher electron density at filling factors in this layer $\nu_{\rm TL}$ equal to 2 and 1. This observation allows the interpretation of fractional states at filling factors $\nu_{\rm Q}=8/3$, 7/3, and 4/3 as combinations of incompressible states of the integer quantum Hall effect in one layer and the fractional quantum Hall effect in the other layer (8/3=2+2/3, 7/3=2+1/3, 4/3=1+1/3). The state of the fractional quantum Hall effect at a total filling factor of 5/4 with an even denominator cannot be interpreted in this way [3] and indicates the existence of unexplored effects of interlayer electron correlation when incompressible state at a filling factor of unity exists in one of the layers. It has been established that incompressible states at $\nu_{\rm TL}=2$ and 1 are broadened in the magnetic field due to the redistribution of electrons between the layers, as a result of which, within one such state, two different fractional quantum Hall effect states can be observed (states at total filling factors $\nu_{\rm Q}=7/3$ and 8/3 in the figure).

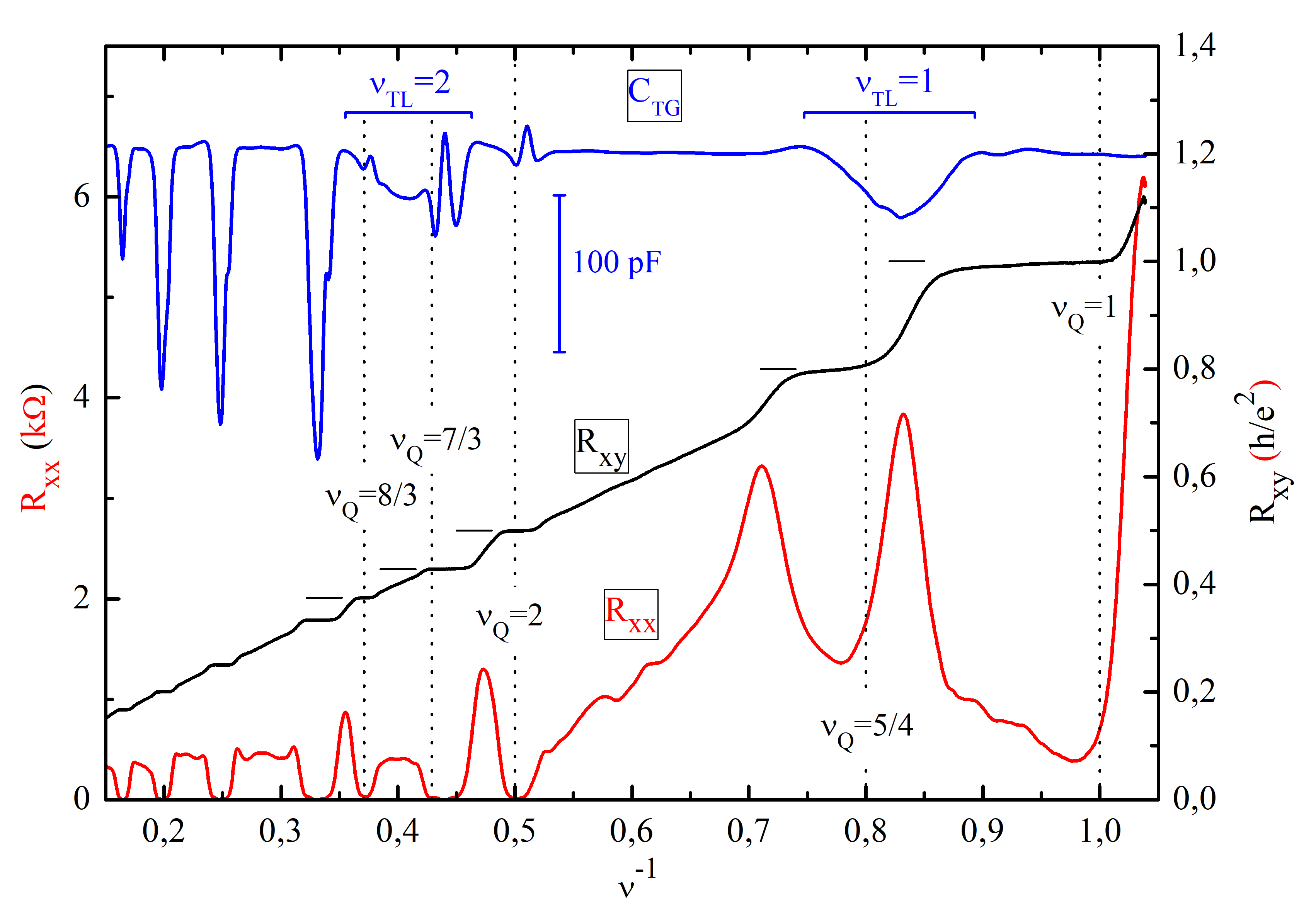
The magnetoresistance $R_{\rm xx}$, Hall resistance $R_{\rm xy}$, and magnetocapacitance $C_{\rm TG}$ between the top gate and the electron system versus inverse value $\nu^{-1}$ of the total filling factor $\nu$, which is proportional to the magnetic field component perpendicular to the system. The vertical dashed lines mark the expected positions $\nu_{\rm Q}$ of several quantum Hall effect states. The values of the quantum plateaus $R_{\rm xy}=\nu_{\rm Q}^{-1}h/e^2$ for these states are shown by the horizontal segments. The horizontal brackets mark the broad magnetocapacitance minima corresponding to incompressible states in the top electron layer at filling factors $\nu_{\rm TL}=2$ and 1. The tilt angle is equal to $45^{\circ}$, temperature $T=45$~mK.

1. S. I. Dorozhkin, A. A. Kapustin, I. B. Fedorov, V. Umansky, K. von Klitzing, and J.H. Smet, J. Appl. Phys. 123, 084301 (2018)
       2. S. I. Dorozhkin, A. A. Kapustin, I. B. Fedorov, V. Umansky, and J.H. Smet, Phys. Rev. B 102, 235307 (2020)
       3. S. I. Dorozhkin, A. A. Kapustin, I. B. Fedorov, V. Umansky, and J.H. Smet, JETP Lett. 117, 68 (2023)

S. I. Dorozhkin, A. A. Kapustin,  and J.H. Smet
JETP Letters 122, issue 7 (2025)