It was shown recently that such a well-known quasi-one-dimensional conductor as (TaSe$_4)_2$I is a Weyl semimetal. Do the properties associated with the topological non-triviality of this material survive in the Peierls state when the Weyl points disappear because of the Peierls gap opening? In this letter, we  present the results of such an investigation performed on (TaSe$_4)_2$I crystals. Longitudinal magnetoresistance of studied samples in all known modes of charge-density wave motion (pinned, creeping, sliding and the ''Fröhlich superconductivity'' ) is small, positive and thus reveals no signature of the chiral anomaly. In order to check a possible contribution of charge density wave defects (dislocations, solitons), similar measurements were undertaken in focused ion beam shaped samples. In such samples, charge-density wave current motion is spatially nonuniform and accompanied by nucleation of numerous charge-density wave defects. A weak localization-like non-parabolic longitudinal magnetoresistance is found to appear in relatively small magnetic fields $B\lesssim 4$ T in the nonlinear conduction regime in the temperature range 70-120 K, whereas weak antilocalization-like behavior dominates at lower temperatures in such samples.  Possible role of the charge-density wave defects is analyzed. Our results differ significantly from ones obtained earlier and raise the question concerning conditions for observation of the chiral anomaly in Weyl semimetals in the Peierls state.

Image of a focused-ion beam proled sample (W-type sample)

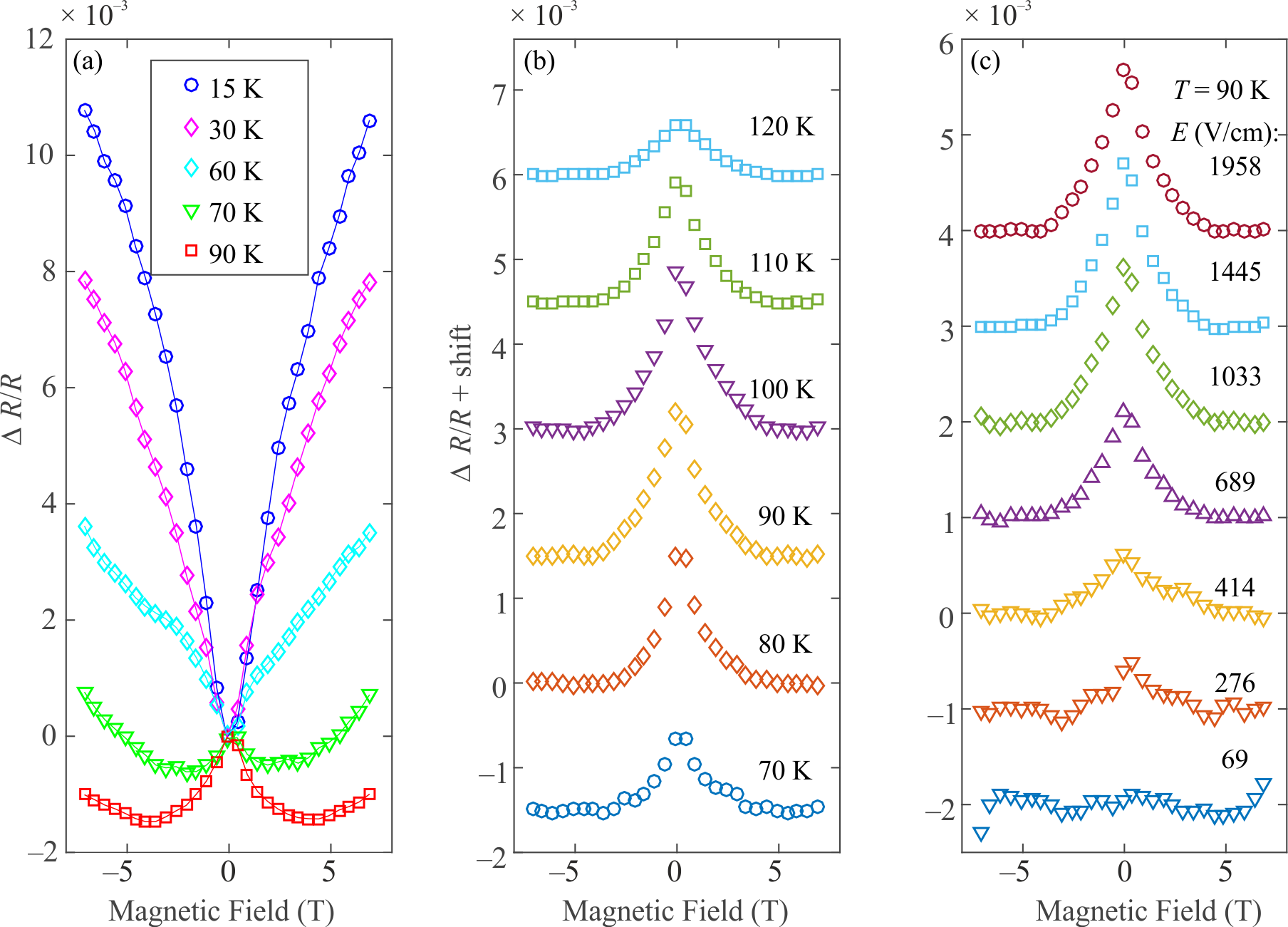
a) Temperature evolution of the longitudinal magnetoresistance in CDW sliding regime. (b-c) Evolution of the negative magnetoresistance contribution with temperature (b) and the electric field (c). W-type sample.

I.A. Cohn, S.G. Zybtsev, A.P. Orlov and S.V. Zaitsev-Zotov
JETP Letters 112, issue 3 (2020)