Multicharged ions, positive ions with a large ionization multiplicity, play a significant role in the processes occurring in high-temperature laboratory and astrophysical plasma. Their properties are important for X-ray astronomy and astrophysics, in the physics of ion thermonuclear fusion, for the study of the interaction of ions with matter, in medicine, etc.

Among the most important characteristics of ions are their potentials (in volts) or ionization energies (in electron volts) numerically coinciding with them. For light elements, almost all ionization energies have been experimentally measured, but in medium and heavy ions, only the first few have been measured. These values for multicharged ions are obtained either by semiempirical methods or as a result of the application of various theoretical models.

The totality of available data on the ionization energies $I_{N_e}(Z)$ (eV) of atoms and ions for elements with atomic numbers $Z \leq 110 $ is presented in the tables of National Institute of Standards and Technology (NIST). However, the use of extensive tables in practice is not very convenient. The need for a sufficiently accurate approximation of tabular data determined the motivation of our study, which considered ions with the number of electrons $N_e\leq 46$ of elements with atomic numbers of $55 \leq Z \leq 95$.

Ions are often considered in isoelectronic series, grouped by the number of electrons $N_e$ in them coinciding with their number in neutral atoms. For example, hydrogen-like ions with $N_e=1$, helium-like ions with $N_e=2$, and so on.
In our work it is shown that in such series the atomic number similarity law is fulfilled. This means that the ionization potentials of the ions in the reduced coordinates are almost parallel lines that are well approximated by quadratic polynomials (see Fig.1).  This makes it possible, knowing the ionization potentials of several elements of the isoelectronic series, to estimate with good accuracy the ionization potentials of ions for other elements.

However, information is usually required on the ionization potentials of an element with an atomic number of $Z$ depending on the number of electrons $N_e$ in the ion. Therefore, the next step was to analyze the dependence of quadratic interpolation coefficients on the number of electrons.   Their polynomial interpolation made it possible to estimate the ionization energies of 1886 ions with an accuracy of a fraction of a percent on the basis of four small tables.

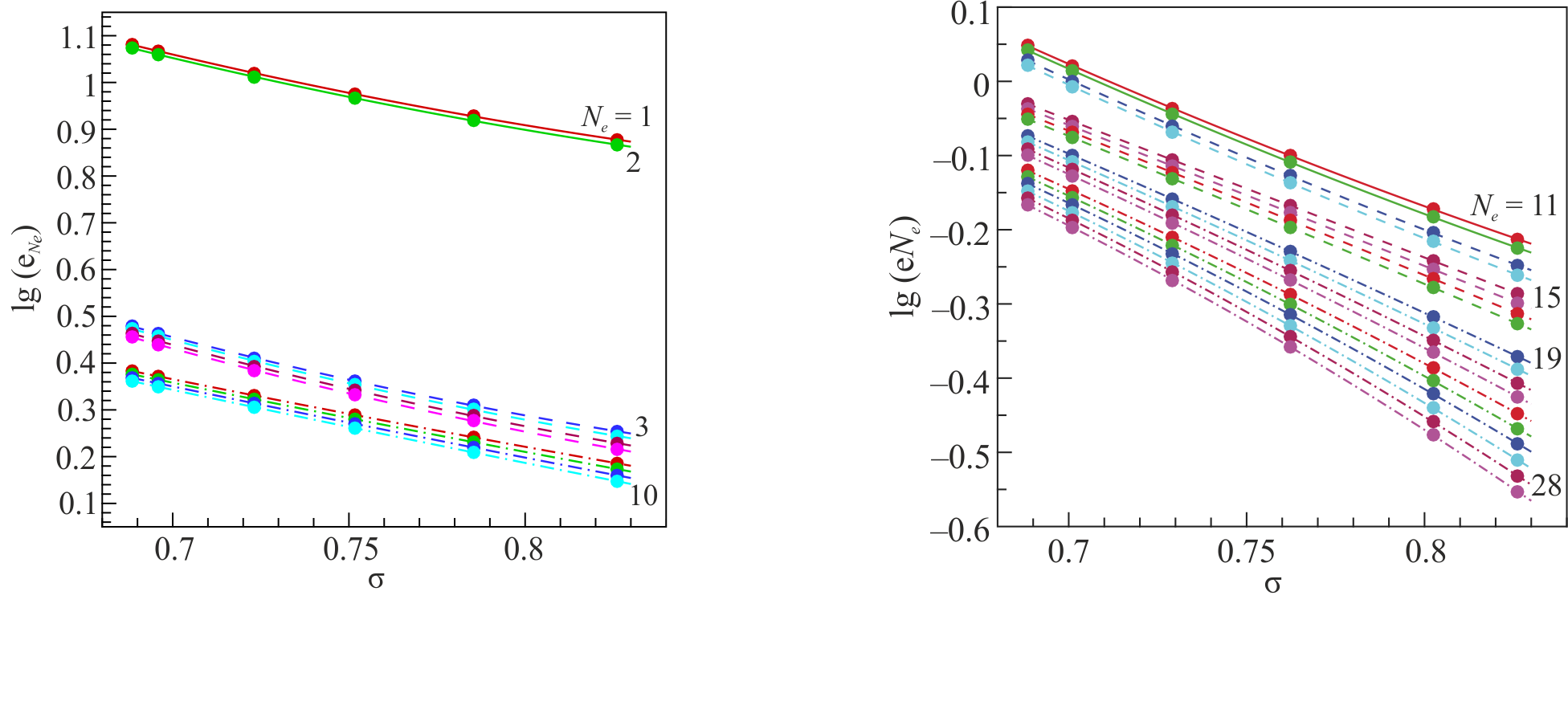
Ionisation energies from database NIST (symbols) in the reduced coordinates. $K$ and $L$ shells are on the left,  $M$ shell is on the right. Lines are quadratic interpolations.

G.V.Shpatakovskaya
JETP Letters 114, issue12 (2021)