We study the kinetics of long-lived cyclotron spin-flip collective exitations  in a purely electronic quantum Hall system with filling factor $\nu=2$. The initial coherent state of the excitations with zero two-dimensional wave vector induced by laser pumping is stochastized over time due to emission of acoustic phonons. The elementary emission process requires participation of two excitations. So the effective rate of phonon emission is proportional to the excitation density squared, and the stochastization process occurs nonexponentially with time. The final distribution of these excitations over 2D momenta, established as a result of stochastization at zero temperature, is compared with equilibrium distribution at finite temperatures.

It is known that the lifetime of considered excitations (purely electronic spin-cyclotron excitons, SCEs) reaches a record magnitude, up to $1\,$ms, in a spin-unpolarised quantum Hall system.  The decay of an initial coherent multi-excitonic state, where all excitations have equal 2D momenta ${\bf q}\!=\!0$, occurs into a diffusive incoherent state provided that the total number of excitations remains constant. When the `zero momentum' ensemble becomes stochastic, the main mass of excitons in the $K$-space diffuses to the vicinity of their energy $q$-dispersion minimum corresponding to a finite absolute value $q\!\approx\!0.9/l_B$ ($l_B$ is the magnetic length). In the future, the diffuse state is thermalized, and finally SCEs completely relax/annihilate. The stochastization occurs without any change of the spin state, thus, certainly, it is much faster than the total SCE-relaxation process. However, the stochastization is associated with emission of phonons and limited by the laws of conservation of energy and momentum. In the  translationary invariant system, the one-exciton process associated with the emission of a phonon is kinematically forbidden: the energy and momentum preservation conditions are never fulfilled in the case.
We calculate the total probability $R_{ p}$ of transition of the coherent state to a state, where, due to the phonon emission, two SCEs acquire nonzero momenta, and one of them has a fixed value: ${\bf q}\!=\!{\bf p}$ .

The physical meaning of the value $R_{p}$  is that it represents the rate of appearance of a SCE with momentum ${\bf p}$ due to the considered process of direct transition from the coherent state. When studying the problem kinetically, it will mean the rate of filling of a `one-particle' excitonic state with specific momentum  $p$. The total stochastization rate induced by phonon-emission, $R\!=\!\sum_{\bf p}R_p$, is the rate of appearance of nonzero-momentum SCEs.  When dividing the `partial' rate $R_p$ by the total one $R$ we obtain a `one-particle' distribution function $F_p$ of nonzero excitons.
Value $F_p$ is time-independent and represents the final distribution function when only non-coherent excitations with nonzero momenta are present in the system. Our approach is suitable if the temperature is sufficiently low to ignore any phonon-absorption processes. In this case thermalization in the studied electron system should be a much longer process than the stochastization considered. It is interesting to compare the distribution function established due to stochastization to a thermodynamically equilibrium distribution corresponding to some temperature. The latter should be Boltzmann due to the assumed rarefaction of the exitonic gas. The time dependence of the coherent ensemble decay is parameterized by value ${\cal T}$ calculated for a specific GaAs/AlGaAs quantum well (see Fig. 1). The number of zero excitons decreases by half during time ${\cal T}\!/n(0)$ where $n(0)$ is the initial SCE concentration with respect to the density of magnetic flux quanta. A tenfold decrease takes time  $\approx\!10{\cal T}\!/n(0)$, therefore, for $n(0)\!\leqslant\!0.01$ it occurs during $\gtrsim\!1\,\mu$s.

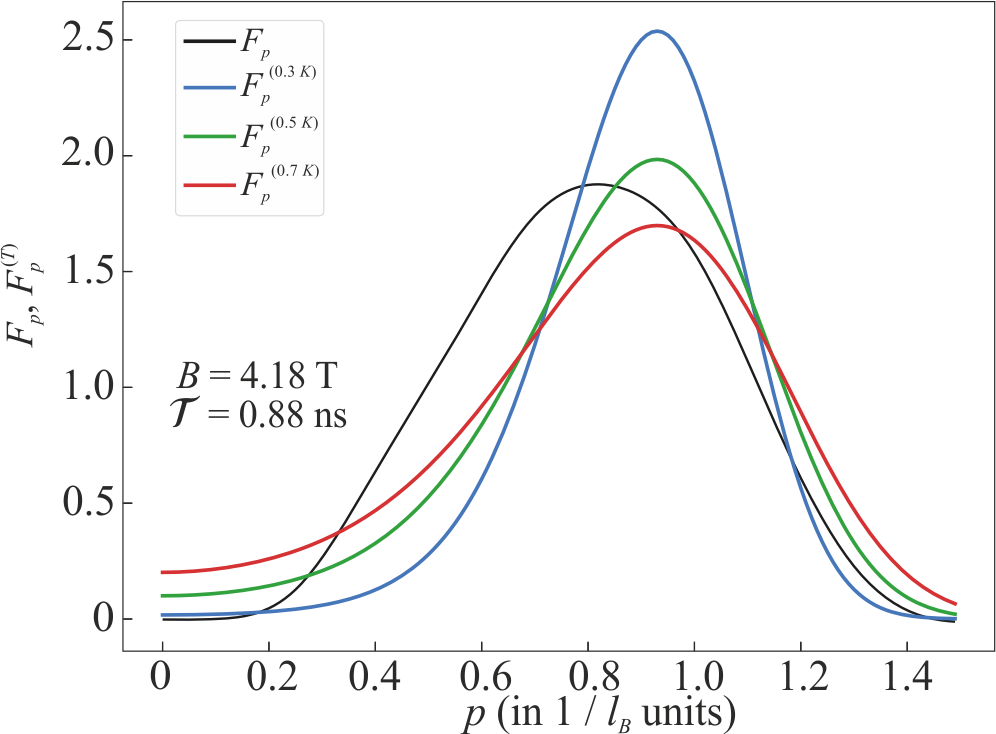
Caculated function $F_p$ of SCEs emerging due to the stochastization process (the black line), and the thermodynamically equilibrium distribution functions $F_p^{(T)}$ at different temperatures. All graphs correspond to $B=4.18\,$T. 

Dickmann S., Kaysin B.D.
JETP Letters 114, issue 10 (2021)