Home
For authors
Submission status

Current
Archive (English)
Archive
   Volumes 61-80
   Volumes 41-60
   Volumes 21-40
   Volumes 1-20
   Volumes 81-92
      Volume 92
      Volume 91
      Volume 90
      Volume 89
      Volume 88
      Volume 87
      Volume 86
      Volume 85
      Volume 84
      Volume 83
      Volume 82
      Volume 81
Search
VOLUME 83 (2006) | ISSUE 5 | PAGE 238
Differential approximation for Kelvin-wave turbulence
PACS: 67.40.Vs
Abstract
I present a nonlinear differential equation model (DAM) for the spectrum of Kelvin waves on a thin vortex filament. This model preserves the original scaling of the six-wave kinetic equation, its direct and inverse cascade solutions, as well as the thermodynamic equilibrium spectra. Further, I extend DAM to include the effect of sound radiation by Kelvin waves. I show that, because of the phonon radiation, the turbulence spectrum ends at a maximum frequency 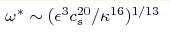\omega^* \sim(\epsilon^3 c_s^{20} / \kappa^{16})^{1/13} where ε is the total energy injection rate, cs is the speed of sound and κ is the quantum of circulation.