
| VOLUME 86 (2007) | ISSUE 7 | PAGE 558 |
|---|
|
On an explicit construction of Parisi landscapes in finite dimensional Euclidean spaces
Y. V. Fyodorov+*, J.-P. Bouchaud
 + Institut für Theoretische Physik, Universität zu Köln, 50937 Köln, Germany * School of Mathematical Sciences, University of Nottingham, Nottingham NG72RD, England  Science & Finance, Capital Fund Management 6-8 Bd Haussmann, 75009 Paris, France Science & Finance, Capital Fund Management 6-8 Bd Haussmann, 75009 Paris, France Service de Physique de l'État Condensé Orme des Merisiers - CEA Saclay, 91191 Gif sur Yvette Cedex, France Service de Physique de l'État Condensé Orme des Merisiers - CEA Saclay, 91191 Gif sur Yvette Cedex, France
ID: 64.60.Cn, 05.40.-a
Abstract
We construct a N-dimensional Gaussian landscape with multiscale, translation invariant, logarithmic correlations and investigate the statistical mechanics of a single particle in this environment. In the limit of high dimension N→ ∞ the free energy of the system in the thermodynamic limit coincides with the most general version of Derrida's Generalized Random Energy Model. The low-temperature behaviour depends essentially on the spectrum of length scales involved in the construction of the landscape. We argue that our construction is in fact valid in any finite spatial dimensions 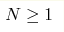 . .
|
 Home
Home