Home
For authors
Submission status

Current
Archive (English)
Archive
   Volumes 61-80
   Volumes 41-60
   Volumes 21-40
   Volumes 1-20
   Volumes 81-92
      Volume 92
      Volume 91
      Volume 90
      Volume 89
      Volume 88
      Volume 87
      Volume 86
      Volume 85
      Volume 84
      Volume 83
      Volume 82
      Volume 81
Search
VOLUME 86 (2007) | ISSUE 10 | PAGE 713
Universal description of the rotational-vibrational spectrum of three particles with zero-range interactions
PACS: 03.65.Ge, 03.75.Ss, 21.45.+v, 36.90.+f
Abstract
A comprehensive universal description of the rotational-vibrational spectrum for two identical particles of mass m and the third particle of mass m1 in the zero-range limit of the interaction between different particles is given for arbitrary values of the mass ratio m/m1 and the total angular momentum L. It is found that the number of vibrational states is determined by the functions Lc(m/m1) and Lb(m/m1). Explicitly, if the two-body scattering length is positive, the number of states is finite for 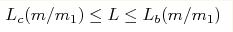L_c(m/m_1) \le L \le L_b(m/m_1), zero for L > Lb(m/m1), and infinite for L < Lc(m/m1). 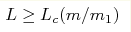If the two-body scattering length is negative, the number of states is zero for L \ge L_c(m/m_1) and infinite for L < Lc(m/m1). 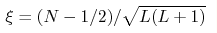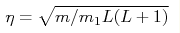For the finite number of vibrational states, all the binding energies are described by the universal function \varepsilon_{L N}(m/m_1) = {\cal E}(\xi, \eta), where \xi = {(N - 1/2)}/{\sqrt{L(L + 1)}}, \eta =\sqrt{{m}/{m_1 L (L + 1)}}, and N is the vibrational quantum number. This scaling dependence is in agreement with the numerical calculations for L > 2 and only slightly deviates from those for L = 1, 2. 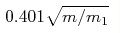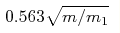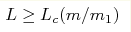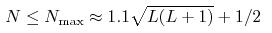The universal description implies that the critical values Lc(m/m1) and Lb(m/m1) increase as 0.401 \sqrt{m/m_1} and 0.563 \sqrt{m/m_1}, respectively, while the number of vibrational states for L \ge L_c(m/m_1) is within the range N \le N_{\max} \approx 1.1 \sqrt{L(L + 1)} + 1/2.