JETP Letters: issues online

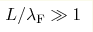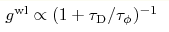We investigate dephasing in open quantum chaotic systems in the limit of large system size to Fermi wavelength ratio, $L/\lambda_{\rm F} \gg 1$ . We semiclassically calculate the weak localization correction g^wl to the conductance for a quantum dot coupled to (i) an external closed dot and (ii) a dephasing voltage probe. 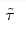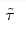In addition to the universal algebraic suppression $g^{\rm wl} \propto (1+\tau_{\rm D}/\tau_\phi)^{-1}$ with the dwell time τ_D through the cavity and the dephasing rate τ_φ^-1, we find an exponential suppression of weak localization by a factor $\propto \exp[-\tilde{\tau}/\tau_\phi]$ , with a system-dependent $\tilde{\tau}$ . In the dephasing probe model, $\tilde{\tau}$ coincides with the Ehrenfest time, $\tilde{\tau} \propto \ln [L/\lambda_{\rm F}]$ , for both perfectly and partially transparent dot-lead couplings. In contrast, when dephasing occurs due to the coupling to an external dot, $\tilde{\tau} \propto \ln [L/\xi]$ depends on the correlation length ξ of the coupling potential instead of λ_F.