
| VOLUME 87 (2008) | ISSUE 4 | PAGE 225 |
|---|
|
Бифуркации и устойчивость поверхностных солитонов огибающих для жидкости конечной глубины
Д. С. Агафонцев
Институт теоретической физики им. Л.Д.Ландау РАН, 119334 Москва, Россия ID: 05.45.Yv, 47.20.Ky, 47.55.Dr
Abstract
Исследуется динамика квазимонохроматических поверхностных гравитационных волн для жидкости конечной глубины при произведении волнового числа и глубины жидкости, близком к критическому 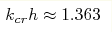 . В
рамках гамильтонова формализма выведено обобщенное нелинейное уравнение
Шредингера, которое по сравнению с классическим НУШ учитывает градиентные члены
к четырехволновому взаимодействию, а также шестиволновое взаимодействие. С
помощью полученного уравнения исследованы модуляционная неустойчивость
монохроматических волн, а также бифуркации солитонных решений и их
устойчивость. Показано, что в случае фокусирующей нелинейности солитоны
устойчивы относительно конечных возмущений, тогда как в случае
дефокусирующей - неустойчивы. . В
рамках гамильтонова формализма выведено обобщенное нелинейное уравнение
Шредингера, которое по сравнению с классическим НУШ учитывает градиентные члены
к четырехволновому взаимодействию, а также шестиволновое взаимодействие. С
помощью полученного уравнения исследованы модуляционная неустойчивость
монохроматических волн, а также бифуркации солитонных решений и их
устойчивость. Показано, что в случае фокусирующей нелинейности солитоны
устойчивы относительно конечных возмущений, тогда как в случае
дефокусирующей - неустойчивы.
|
 Home
Home