JETP Letters: issues online

We propose a random matrix approach to describe vibrations in disordered systems. The dynamical matrix M is taken in the form M=AA^T where A is a real random matrix. It guaranties that M is a positive definite matrix. This is necessary for mechanical stability of the system. We built matrix A on a simple cubic lattice with translational invariance and interaction between nearest neighbors. It was found that for a certain type of disorder acoustical phonons cannot propagate through the lattice and the density of states g(ω) is not zero at ω=0. The reason is a breakdown of affine assumptions and inapplicability of the macroscopic elasticity theory. Young modulus goes to zero in the thermodynamic limit. It reminds of some properties of a granular matter at the jamming transition point. Most of the vibrations are delocalized and similar to diffusons introduced by Allen, Feldman et al., Phil. Mag. B 79, 1715 (1999). We show how one can gradually return rigidity and phonons back to the system increasing the width of the so-called phonon gap (the region where 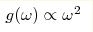$g(\omega)\propto\omega^2$ ). Above the gap the reduced density of states g(ω)/ω² shows a well-defined Boson peak which is a typical feature of glasses. Phonons cease to exist above the Boson peak and diffusons are dominating. It is in excellent agreement with recent theoretical and experimental data.