Home
| VOLUME 100 (2014) | ISSUE 4 | PAGE 297 |
|---|
|
Towards matrix model representation of HOMFLY polynomials
A. Alexandrov+*×, A. Mironov×°, A. Morozov×, And. Morozov
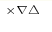 +Freiburg Institute for Advanced Studies, University of Freiburg, 79104 Freiburg, Germany *Mathematics Institute, University of Freiburg, 79104 Freiburg, Germany ×Alikhanov Institute of theoretical and Experimental Physics, 123182 Moscow, Russia °Lebedev Physics Institute, 119991 Moscow, Russia ∇Lomonosov MSU, 119991 Moscow, Russia  Laboratory of Quantum Topology, Chelyabinsk State University, Chelyabinsk, Russia
Abstract
We investigate possibilities of generalizing the TBEM (Tierz, Brini-Eynard-Mari 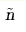 o) eigenvalue
matrix model, which represents
the non-normalized colored HOMFLY polynomials for torus knots
as averages of the corresponding characters.
We look for a model of the same type, which
is a usual Chern-Simons mixture of the Gaussian potential,
typical for Hermitean models, and the sine Vandermonde factors, typical
for the unitary ones.
We mostly concentrate on the family of twist knots,
which contains a single torus knot, the trefoil.
It turns out that for the trefoil the TBEM measure
is provided by an action of Laplace exponential
on the Jones polynomial.
This procedure can be applied to arbitrary knots
and provides a TBEM-like integral representation
for the N=2 case.
However, beyond the torus family,
both the measure and its lifting to larger N
contain non-trivial corrections in  .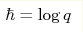
A possibility could be to absorb these corrections
into a deformation of the Laplace evolution by higher
Casimir and/or cut-and-join operators,
in the spirit of Hurwitz τ-function approach to knot theory,
but this remains a subject for future investigation.
|