
| VOLUME 102 (2015) | ISSUE 3 | PAGE 216 |
|---|
|
Простой контрпример для
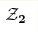 -классификации топологических изоляторов, основанной на соответствии объем-граница -классификации топологических изоляторов, основанной на соответствии объем-граница
С. Н. Молотков+*×, М. И. Рыжкин+
+Институт физики твердого тела РАН, 142432 Черноголовка, Россия *Академия криптографии РФ, 121552 Москва, Россия ×Факультет вычислительной математики и кибернетики, МГУ им. Ломоносова, 119991 Москва, Россия
Abstract
Ранее была предложена так называемая 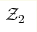 -классификация
топологических изоляторов, основанная на соответствии объем-граница
(bulk-boundary correspondence), которая считается общепринятой и
сводится к следующим утверждениям:
1) nontrivial -классификация
топологических изоляторов, основанная на соответствии объем-граница
(bulk-boundary correspondence), которая считается общепринятой и
сводится к следующим утверждениям:
1) nontrivial 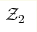 invariants imply the existence of gapless
surface states, 2) the invariants imply the existence of gapless
surface states, 2) the 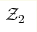 invariants can be deduced from the
topological
structure of the Bloch wave functions of the bulk crystal in
the Brillouin zone
(L. Fu and C. L. Kane, Phys. Rev. B 76, 045302 (2007)).
В данной работе приводится простой контрпример для invariants can be deduced from the
topological
structure of the Bloch wave functions of the bulk crystal in
the Brillouin zone
(L. Fu and C. L. Kane, Phys. Rev. B 76, 045302 (2007)).
В данной работе приводится простой контрпример для 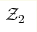 -классификации.
Показано, что при одном и том же объеме, одной и той же
пространственной симметрии полубесконечного кристалла и, соответственно,
тривиальном значении -классификации.
Показано, что при одном и том же объеме, одной и той же
пространственной симметрии полубесконечного кристалла и, соответственно,
тривиальном значении 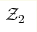 -инварианта (тривиальном классе
эквивалентности объемного гамильтониана) для 3 -инварианта (тривиальном классе
эквивалентности объемного гамильтониана) для 3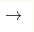 2D-системы на
поверхностях могут существовать как топологически устойчивые, так и
топологически неустойчивые поверхностные состояния. Более того, топологически
устойчивые поверхностные состояния могут существовать как при тривиальном
(поверхность Bi(111)), так и при нетривиальном
(поверхность Sb(111)) значениях объемного 2D-системы на
поверхностях могут существовать как топологически устойчивые, так и
топологически неустойчивые поверхностные состояния. Более того, топологически
устойчивые поверхностные состояния могут существовать как при тривиальном
(поверхность Bi(111)), так и при нетривиальном
(поверхность Sb(111)) значениях объемного 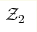 -инварианта.
Данные факты ставят под сомнение утверждение о том, что -инварианта.
Данные факты ставят под сомнение утверждение о том, что
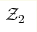 -классификация, основанная на соответствии объем-граница,
отвечает за появление и топологическую устойчивость поверхностных состояний. -классификация, основанная на соответствии объем-граница,
отвечает за появление и топологическую устойчивость поверхностных состояний.
|
 Home
Home