
| VOLUME 103 (2016) | ISSUE 2 | PAGE 124 |
|---|
|
Long-range spin correlations in a honeycomb spin model with magnetic field
A. V. Lunkin+*, K. S. Tikhonov+*, M. V. Feigel'man+*
+Landau Institute for Theoretical Physics of the RAS, 119334 Moscow, Russia *Moscow Institute of Physics and Technology, 141700 Moscow, Russia
Abstract
We consider spin-1/2 model on the honeycomb lattice (Ann. Phys. 321, 2 (2006)) in presence of weak magnetic field  .
Such a perturbation treated in the lowest nonvanishing order over hα
leads (Phys. Rev. Lett. 106, 067203 (2011))
to a power-law decay of irreducible spin correlations .
Such a perturbation treated in the lowest nonvanishing order over hα
leads (Phys. Rev. Lett. 106, 067203 (2011))
to a power-law decay of irreducible spin correlations
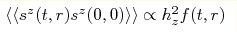 , where , where ![f(t,r)\propto \lbrack \max (t,Jr)]^{-4}](/img/latex/e7/e7b0c240eec414cd8ea1b4f0eba838a0-v2.png) .
In the present Letter we studied the effects of the next order of
perturbation
in hz and found an additional term of the order hz4 in the correlation
function .
In the present Letter we studied the effects of the next order of
perturbation
in hz and found an additional term of the order hz4 in the correlation
function 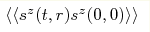 which scales as which scales as
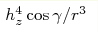 at at 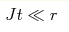 , where γ is the polar
angle in the 2D plane. We demonstrate that such a contribution can be
understood
as a result of a perturbation of the effective Majorana Hamiltonian by
weak imaginary vector potential , where γ is the polar
angle in the 2D plane. We demonstrate that such a contribution can be
understood
as a result of a perturbation of the effective Majorana Hamiltonian by
weak imaginary vector potential 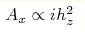 . .
|
 Home
Home