
| VOLUME 104 (2016) | ISSUE 12 | PAGE 875 |
|---|
|
Некоторые точные решения уравнения локальной индукции для движения вихря в бозе-конденсате с гауссовым профилем плотности
В. П. Рубан
Институт теоретической физики им. Л.Д. Ландау РАН, 142432 Черноголовка, Россия
Abstract
Рассмотрена динамика вихревой нити в бозе-конденсате, равновесная плотность которого во вращающейся с угловой скоростью Ω системе координат является гауссовой с квадратичной формой 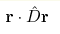 .
Показано, что уравнение движения нити в приближении локальной индукции
допускает класс точных решений в виде прямого вихря
R(β,t)=β M(t) + N(t),
где β - продольный параметр, t - время.
Вихрь скользит по поверхности эллипсоида, что следует из законов
сохранения .
Показано, что уравнение движения нити в приближении локальной индукции
допускает класс точных решений в виде прямого вихря
R(β,t)=β M(t) + N(t),
где β - продольный параметр, t - время.
Вихрь скользит по поверхности эллипсоида, что следует из законов
сохранения 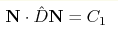 и и
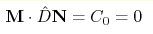 .
Уравнение эволюции касательного вектора M(t)
оказывается замкнутым и имеет интегралы движения .
Уравнение эволюции касательного вектора M(t)
оказывается замкнутым и имеет интегралы движения
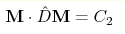 , ,
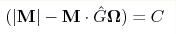 , где матрица , где матрица
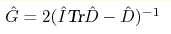 . Пересечение
соответствующих поверхностей уровня
определяет траектории в фазовом пространстве. . Пересечение
соответствующих поверхностей уровня
определяет траектории в фазовом пространстве.
|
 Home
Home