Home
For authors
Submission status

Archive
Archive (English)
Current
   Volumes 113-120
   Volumes 93-112
      Volume 112
      Volume 111
      Volume 110
      Volume 109
      Volume 108
      Volume 107
      Volume 106
      Volume 105
      Volume 104
      Volume 103
      Volume 102
      Volume 101
      Volume 100
      Volume 99
      Volume 98
      Volume 97
      Volume 96
      Volume 95
      Volume 94
      Volume 93
Search
VOLUME 112 (2020) | ISSUE 6 | PAGE 388
Зеркальные пары орбифолдов квинтики
DOI: 10.31857/S1234567820180111
Abstract
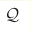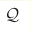В этой работе мы сравниваем две конструкции построения зеркальных пар многообразий Калаби-Яу на примере орбифолдов Квинтики \mathcal{Q}. Первая - конструкция Берглунда-Хубша-Кравитца (БХК) состоит в следующем. Мы рассматриваем фактор X гиперповерхности \mathcal{Q} по некоторой подгруппе H' максимально допустимой группы SL. Тогда зеркальное многообразие Y определяется как фактор по дополнительной подгруппе H'T. Вторая - конструкция Батырева определяет по данным полинома WX, задающего Калаби-Яу X, торическое многообразие T, содержащее зеркало Y как гиперповерхность, задаваемую нулями полинома WY. Сам полином WY мы находим в явном виде. По виду WY мы находим его группу симметрии и проверяем, что она совпадает с предсказанной конструкцией БХК.