
| VOLUME 113 (2021) | ISSUE 9 | PAGE 589 |
|---|
|
Understanding two slopes in the
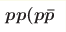 ) differential cross sections ) differential cross sections
Yu. A. Simonov
National Research Centre "Kurchatov Institute" - ITEP, 117259 Moscow, Russia
Abstract
Recent experiments have discovered two exponents in the pp elastic differential cross sections with two different slope parameters, of the order (16-20) GeV-2 and (4-4.8) GeV-2 in the regions 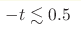 GeV2 and GeV2 and
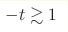 GeV2, respectively. We suggest a simple model of the pp
elastic scattering with two types of particle
exchanges: 1) when the exchanged particle transfers the momentum Q
from a quark of the proton p1 to one quark in another proton p2,
producing the slope B1;
2) when the transfer occurs from two quarks in the p1 to two quarks in
the p2, giving the exponent with the slope B2. The resulting
amplitude is proportional to
the product of the form factors of two protons, depending on Q, but
with different coefficients in the cases 1) and 2). Using the only
parameter - the proton
charge radius r2ch= 0.93 fm2, one obtains B1 = 16 GeV-2,
B2 = 4 GeV-2 with the strict value of the ratio, GeV2, respectively. We suggest a simple model of the pp
elastic scattering with two types of particle
exchanges: 1) when the exchanged particle transfers the momentum Q
from a quark of the proton p1 to one quark in another proton p2,
producing the slope B1;
2) when the transfer occurs from two quarks in the p1 to two quarks in
the p2, giving the exponent with the slope B2. The resulting
amplitude is proportional to
the product of the form factors of two protons, depending on Q, but
with different coefficients in the cases 1) and 2). Using the only
parameter - the proton
charge radius r2ch= 0.93 fm2, one obtains B1 = 16 GeV-2,
B2 = 4 GeV-2 with the strict value of the ratio,
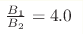 , independent of rch. These predictions are
surprisingly close to the data both in the pp and in the , independent of rch. These predictions are
surprisingly close to the data both in the pp and in the  differential cross sections. Comparison
to experimental data and theoretical approaches is discussed, together
with possible implications for the future development of the theory.
differential cross sections. Comparison
to experimental data and theoretical approaches is discussed, together
with possible implications for the future development of the theory.
|
 Home
Home