 Home |
| For authors |
| Submission status |
| Archive
|
| Archive
(English)
|
| Current
|
| Volumes 93-112 |
 Volumes 113-120 |
| Volume 120 |
| Volume 119 |
| Volume 118 |
| Volume 117 |
| Volume 116 |
| Volume 115 |
| Volume 114 |
| Volume 113 |
| Search |
| VOLUME 115 (2022) | ISSUE 1 | PAGE 59 |
|---|
|
Tеория голоморфных отображений двумерных комплексных многообразий в торические многообразия и теория мультиструн типа А
О. С. Чекересa, А. С. Лосевb,c,d 1), П. Н. Мневe,f 1), Д. Р. Юмансg 1)
aUniversity of Connecticut, Department of Mathematics, Storrs, CT 06269, USA bWu Wen-Tsun Key Lab of Mathematics, Chinese Academy of Sciences, USTC, Hefei, 230026, Anhui, P.R.China cНациональный исследовательский университет "Высшая школа экономики" Лаборатория зеркальной симметрии НИУ ВШЭ, 119048 Москва, Россия dНаучно-исследовательский институт системных исследований РАН (ФГУ ФНЦ НИИСИ РАН), 117218 Москва, Россия eUniversity of Notre Dame, Notre Dame, IN 46556, USA fСанкт-Петербургское отделение Математического института им. В. А. Стеклова РАН, 191023 С.-Петербург, Россия gAlbert Einstein Center for Fundamental Physics, Institute for Theoretical Physics, University of Bern, 3012 Bern, Switzerland
Abstract
Мы изучаем обобщение A-модели - теорию поля, локализующуюся на голоморфные отображения комплексных многообразий размерности 2 в торический таргет. Поля модели - отображения в 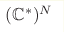 , и мы
вставляем специальные наблюдаемые на вещественно-двумерных
подмногообразиях типа (1, 1). Эти наблюдаемые эффективно описывают
отображения на торическую компактификацию. Мы также строим зеркально
двойственную модель. Оказывается, что это свободная теория,
взаимодействующая с Ncomp топологическими струнами типа A. Здесь
Ncomp - число компактифицирующих дивизоров торического таргета.
До зеркального преобразования эти струны являются вихревыми (более точно,
голомортексными) струнами.
|