
| VOLUME 115 (2022) | ISSUE 10 | PAGE 610 |
|---|
|
On Lorentz invariance and the minimum length1)
M. D. Pollock2)
V. A. Steklov Mathematical Institute, Russian Academy of Sciences, 119991 Moscow, Russia
Abstract
It was shown by Kirzhnits and Chechen, following an earlier paper by Mead, that the minimum length scale l is constrained by the Mössbauer effect, which leads to the result  cm, assuming the Snyder
discrete space-time and conventional nuclides. Here, we note, firstly,
that some recently discussed nuclides,
for example 18976Os, have much narrower natural line
widths, which, if excited by synchrotron radiation,
could potentially decrease the limiting value to cm, assuming the Snyder
discrete space-time and conventional nuclides. Here, we note, firstly,
that some recently discussed nuclides,
for example 18976Os, have much narrower natural line
widths, which, if excited by synchrotron radiation,
could potentially decrease the limiting value to  cm
in future experiments. The Snyder space-time
and the superstring theory are both locally Lorentz invariant, and give
rise to the same form of generalized indeterminacy
principle, if we set cm
in future experiments. The Snyder space-time
and the superstring theory are both locally Lorentz invariant, and give
rise to the same form of generalized indeterminacy
principle, if we set 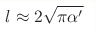 , where α' is
the Regge slope parameter, which is thus also
constrained by the Mössbauer effect. For the heterotic superstring, in
particular, , where α' is
the Regge slope parameter, which is thus also
constrained by the Mössbauer effect. For the heterotic superstring, in
particular,
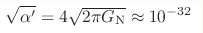 cm, apparently
beyond experimental reach. A hadron
string theory at energy cm, apparently
beyond experimental reach. A hadron
string theory at energy 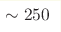 MeV, however, would be ruled out,
since then MeV, however, would be ruled out,
since then  cm. We emphasize
that these results all presuppose a de Sitter momentum space, for the
alternative anti-de Sitter momentum space implies
no minimum length scale, and therefore seems unphysical. cm. We emphasize
that these results all presuppose a de Sitter momentum space, for the
alternative anti-de Sitter momentum space implies
no minimum length scale, and therefore seems unphysical.
|
 Home
Home