JETP Letters: issues online

To regularize the three-body problem, Minlos and Faddeev suggested a modification of zero-range model, which diminishes interaction at the triple-collision point. The analysis reveals that this regularization results in four alternatives depending on the regularization parameter σ . 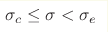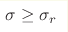Explicitly, Efimov or Thomas effects remain for σ < σ_c , the additional boundary conditions of two types should be imposed at the triple-collision point for $\sigma_c \le \sigma < \sigma_e$ and σ_e < σ < σ_r , and the problem is regularized for $\sigma \ge \sigma_r$ . Critical values σ_c < σ_e < σ_r separating different alternatives are determined both for a two-component three-body system and for three identical bosons.