
| VOLUME 119 (2024) | ISSUE 7 | PAGE 560 |
|---|
|
Devoted to memory of Alexei Alexandrovich Starobinsky De Sitter local thermodynamics in f(R) gravity
G. E. Volovik
Low Temperature Laboratory, Aalto University, P.O. Box 15100, FI-00076 Aalto, Finland Landau Institute for Theoretical Physics, 142432 Chernogolovka, Russia
Abstract
We consider the local thermodynamics of the de Sitter state in the 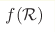 gravity. The local temperature, which is the same for all
points of the de Sitter space, is T=H/π, where H is the Hubble
parameter. It is twice larger than the Gibbons-Hawking temperature of the
cosmological horizon, T GH=H/2π. The local temperature is not
related to the cosmological horizon. It determines the rate of the
activation processes, which are possible in the de Sitter environment.
The typical example is the process of the ionization of the atom in the
de Sitter environment, which rate is determined by temperature T=H/π.
The local temperature determines the local entropy of the de Sitter
vacuum state, and this allows to calculate the total entropy inside the
cosmological horizon. The result reproduces the Gibbons-Hawking area
law, which corresponds to the Wald entropy, S hor=4π KA. Here
K is the effective gravitational coupling, gravity. The local temperature, which is the same for all
points of the de Sitter space, is T=H/π, where H is the Hubble
parameter. It is twice larger than the Gibbons-Hawking temperature of the
cosmological horizon, T GH=H/2π. The local temperature is not
related to the cosmological horizon. It determines the rate of the
activation processes, which are possible in the de Sitter environment.
The typical example is the process of the ionization of the atom in the
de Sitter environment, which rate is determined by temperature T=H/π.
The local temperature determines the local entropy of the de Sitter
vacuum state, and this allows to calculate the total entropy inside the
cosmological horizon. The result reproduces the Gibbons-Hawking area
law, which corresponds to the Wald entropy, S hor=4π KA. Here
K is the effective gravitational coupling, 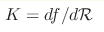 .
In the local thermodynamic approach, K is the thermodynamic variable,
which is conjugate to the Ricci scalar curvature .
In the local thermodynamic approach, K is the thermodynamic variable,
which is conjugate to the Ricci scalar curvature 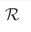 . The
holographic connection between the bulk entropy of the Hubble volume and
the surface entropy of the cosmological horizon supports the suggestion
that the de Sitter quantum vacuum is characterized by the local
thermodynamics with the local temperature T=H/π. The local
temperature T=H/π of the de Sitter vacuum suggests that the de Sitter
vacuum is locally unstable towards the creation of matter and its further
heating. The decay of the de Sitter vacuum due to such processes
determines the quantum breaking time of the space-times with positive
cosmological constant. . The
holographic connection between the bulk entropy of the Hubble volume and
the surface entropy of the cosmological horizon supports the suggestion
that the de Sitter quantum vacuum is characterized by the local
thermodynamics with the local temperature T=H/π. The local
temperature T=H/π of the de Sitter vacuum suggests that the de Sitter
vacuum is locally unstable towards the creation of matter and its further
heating. The decay of the de Sitter vacuum due to such processes
determines the quantum breaking time of the space-times with positive
cosmological constant.
|
 Home
Home