Home
For authors
Submission status

Current
Archive (English)
Archive
   Volumes 81-92
   Volumes 41-60
   Volumes 21-40
   Volumes 1-20
   Volumes 61-80
      Volume 80
      Volume 79
      Volume 78
      Volume 77
      Volume 76
      Volume 75
      Volume 74
      Volume 73
      Volume 72
      Volume 71
      Volume 70
      Volume 69
      Volume 68
      Volume 67
      Volume 66
      Volume 65
      Volume 64
      Volume 63
      Volume 62
      Volume 61
Search
VOLUME 80 (2004) | ISSUE 1 | PAGE 60
Energy absorption in time-dependent unitary random matrix ensembles: dynamic vs. Anderson localization
PACS: 03.65.-w, 72.10.Bg, 73.23.-b
Abstract
We consider energy absorption in an externally driven complex system of noninteracting fermions with the chaotic underlying dynamics described by the unitary random matrices. In the absence of quantum interference the energy absorption rate W(t) can be calculated with the help of the linear-response Kubo formula. We calculate the leading two-loop interference correction to the semiclassical absorption rate for an arbitrary time dependence of the external perturbation. Based on the results for periodic perturbations, we make a conjecture that the dynamics of the periodically-driven random matrices can be mapped onto the one-dimensional Anderson model. We predict that in the regime of strong dynamic localization 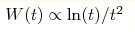W(t)\propto \ln(t)/t^2 rather than decays exponentially.