Home
For authors
Submission status

Current
Archive (English)
Archive
   Volumes 81-92
   Volumes 41-60
   Volumes 21-40
   Volumes 1-20
   Volumes 61-80
      Volume 80
      Volume 79
      Volume 78
      Volume 77
      Volume 76
      Volume 75
      Volume 74
      Volume 73
      Volume 72
      Volume 71
      Volume 70
      Volume 69
      Volume 68
      Volume 67
      Volume 66
      Volume 65
      Volume 64
      Volume 63
      Volume 62
      Volume 61
Search
VOLUME 76 (2002) | ISSUE 11 | PAGE 799
How behavior of systems with sparse spectrum can be predicted on a quantum computer
PACS: 03.67.Lx
Abstract
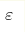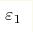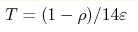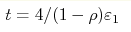Call a spectrum of Hamiltonian H sparse if each eigenvalue can be quickly restored within \varepsilon from its rough approximation within \varepsilon_1 by means of some classical algorithm. It is shown how a behavior of system with sparse spectrum up to time T={(1-\rho)}/{14\varepsilon} can be predicted on a quantum computer with the time complexity t={4}/{(1-\rho)\varepsilon_1} plus the time of classical algorithm, where ρ is the fidelity. The quantum knowledge of Hamiltonian eigenvalues is considered as the new Hamiltonian WH whose action on each eigenvector of H gives the corresponding eigenvalue. Speedup of an evolution for systems with the sparse spectrum is possible because for such systems the Hamiltonian WH can be quickly simulated on the quantum computer. For an arbitrary system (even in the classical case) its behavior cannot be predicted on a quantum computer even for one step ahead. By this method we can also restore the history with the same efficiency.