Home
For authors
Submission status

Current
Archive (English)
Archive
   Volumes 81-92
   Volumes 41-60
   Volumes 21-40
   Volumes 1-20
   Volumes 61-80
      Volume 80
      Volume 79
      Volume 78
      Volume 77
      Volume 76
      Volume 75
      Volume 74
      Volume 73
      Volume 72
      Volume 71
      Volume 70
      Volume 69
      Volume 68
      Volume 67
      Volume 66
      Volume 65
      Volume 64
      Volume 63
      Volume 62
      Volume 61
Search
VOLUME 76 (2002) | ISSUE 12 | PAGE 855
Anticommutativity equation in topological quantum mechanics
PACS: 03.65.-w
Abstract
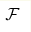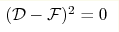We consider the topological quantum mechanics as an example of topological field theory and show that it special properties lead to numerous interesting relations for topological corellators in this theory. We prove that the generating function \mathcal{F} for this correlators satisfies the anticommutativity equation (\mathcal{D}- \mathcal{F})^2=0. We show that commutativity equation [dB,dB]=0 could be considered as a special case of anticommutativity equation.