
| VOLUME 74 (2001) | ISSUE 5 | PAGE 309 |
|---|
|
On critical behavior of phase transitions in certain antiferromagnets with complicated ordering
A. I. Mudrov, K. B. Varnashev1)
Bar-Ilan University, 52900 Ramat-Gan, Israel Saint Petersburg Electrotechnical University, 197376 Saint Petersburg, Russia ID: 64.60.-i, 75.40.Cx
Abstract
Within the four-loop 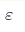 expansion, we study the critical
behavior of certain antiferromagnets with complicated ordering. We show that
an anisotropic stable fixed point governs the phase transitions with new
critical exponents. This is supported by the estimate of critical
dimensionality NcC=1.445(20) obtained from six loops via the exact
relation expansion, we study the critical
behavior of certain antiferromagnets with complicated ordering. We show that
an anisotropic stable fixed point governs the phase transitions with new
critical exponents. This is supported by the estimate of critical
dimensionality NcC=1.445(20) obtained from six loops via the exact
relation 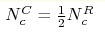 established for the real and complex
hypercubic models. established for the real and complex
hypercubic models.
|
 Home
Home