
| VOLUME 78 (2003) | ISSUE 9 | PAGE 1082 |
|---|
|
Waves in a superlattice with anisotropic inhomogeneities
V. A. Ignatchenko, A. A. Maradudin*, A. V. Poszdnyakov+
L.V.Kirensky Institute of Physics SB RAS, 660036 Krasnoyarsk, Russia *Department of Physics and Astronomy University of California, Irvine, CA, 92697, USA ID: 68.65.-k, 75.30.Ds
Abstract
Dependences of the dispersion laws and damping of waves in an initially sinusoidal superlattice on inhomogeneities with anisotropic correlation properties are studied for the first time. The period of the superlattice is modulated by the random function described by the anisotropic correlation function Kφ( r) that has different correlation radii, 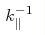 and and 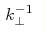 , along the axis of
the superlattice z and in the plane xy, respectively. The
anisotropy of the correlation is characterized by the parameter , along the axis of
the superlattice z and in the plane xy, respectively. The
anisotropy of the correlation is characterized by the parameter
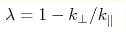 that can change from λ=0 to
λ=1 when the correlation wave number that can change from λ=0 to
λ=1 when the correlation wave number 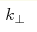 changes from changes from 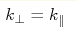 (isotropic 3D inhomogeneities)
to
(isotropic 3D inhomogeneities)
to 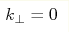 (1D inhomogeneities). The correlation function of the
superlattice K( r) is developed. Its decreasing part
goes to the asymptote L that divides the correlation volume into two parts
characterized by finite and infinite correlation radii.
The dependences of the
width of the gap in the spectrum at the boundary of the Brillouin zone
Δν and the damping of waves ξ on the value of λ are
studied. It is shown that decreasing L leads
to the decrease of Δν and increase of ξ with the increase of λ. (1D inhomogeneities). The correlation function of the
superlattice K( r) is developed. Its decreasing part
goes to the asymptote L that divides the correlation volume into two parts
characterized by finite and infinite correlation radii.
The dependences of the
width of the gap in the spectrum at the boundary of the Brillouin zone
Δν and the damping of waves ξ on the value of λ are
studied. It is shown that decreasing L leads
to the decrease of Δν and increase of ξ with the increase of λ.
|
 Home
Home