
| VOLUME 85 (2007) | ISSUE 10 | PAGE 621 |
|---|
|
Superconductor-insulator duality for the array of Josephson wires
I. V. Protopopov, M. V. Feigel'man
L.D. Landau Institute for Theoretical Physics, 119334 Moscow, Russia Moscow Institute of Physics and Technology, 141700 Dolgoprudny, Moscow Region, Russia ID: 74.40.+k, 74.81.Fa
Abstract
We propose novel model system for the studies of superconductor-insulator transitions, which is a regular lattice, whose each link consists of Josephson-junction chain of 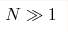 junctions in sequence.
The theory of such an array is developed for the case of semiclassical
junctions with the Josephson energy EJ large compared to the junctions's
Coulomb energy EC = e2/2C.
Exact duality transformation is derived, which
transforms the Hamiltonian of the proposed model into a standard Hamiltonian
of JJ array.
The nature of the ground state
is controlled (in the absence of random offset charges)
by the parameter junctions in sequence.
The theory of such an array is developed for the case of semiclassical
junctions with the Josephson energy EJ large compared to the junctions's
Coulomb energy EC = e2/2C.
Exact duality transformation is derived, which
transforms the Hamiltonian of the proposed model into a standard Hamiltonian
of JJ array.
The nature of the ground state
is controlled (in the absence of random offset charges)
by the parameter 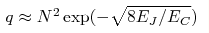 , with superconductive
state corresponding to small q < qc .
The values of qc are calculated
for magnetic frustrations f= 0 and f=1/2.
Temperature of superconductive transition Tc(q) and q < qc is
estimated for the same values of f. In presence of strong random offset
charges, the T=0 phase diagram is controlled by the parameter , with superconductive
state corresponding to small q < qc .
The values of qc are calculated
for magnetic frustrations f= 0 and f=1/2.
Temperature of superconductive transition Tc(q) and q < qc is
estimated for the same values of f. In presence of strong random offset
charges, the T=0 phase diagram is controlled by the parameter
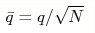 ; we estimated critical value ; we estimated critical value 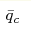 and critical
temperature and critical
temperature 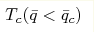 at zero magnetic frustration. at zero magnetic frustration.
|
 Home
Home