Home
For authors
Submission status

Archive
Archive (English)
Current
   Volumes 113-120
   Volumes 93-112
      Volume 112
      Volume 111
      Volume 110
      Volume 109
      Volume 108
      Volume 107
      Volume 106
      Volume 105
      Volume 104
      Volume 103
      Volume 102
      Volume 101
      Volume 100
      Volume 99
      Volume 98
      Volume 97
      Volume 96
      Volume 95
      Volume 94
      Volume 93
Search
VOLUME 93 (2011) | ISSUE 4 | PAGE 213
Numerical study of Fermi-Pasta-Ulam recurrence for water waves over finite depth
Abstract
Highly accurate direct numerical simulations have been performed for two-dimensional free-surface potential flows of an ideal incompressible fluid over a constant depth h, in the gravity field g. In each numerical experiment, at t=0 the free surface profile was in the form 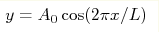y=A_0\cos(2\pi x/L), and the velocity field  v=0. 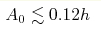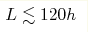The computations demonstrate the phenomenon of Fermi-Pasta-Ulam (FPU) recurrence takes place in such systems for moderate initial wave amplitudes A_0\lesssim 0.12 h and spatial periods at least L\lesssim 120 h. The time of recurrence T FPU is well fitted by the formula T_{\rm FPU}(g/h)^{1/2}\approx 0.16(L/h)^2(h/A_0)^{1/2}.