
| VOLUME 94 (2011) | ISSUE 4 | PAGE 277 |
|---|
|
On kinetic theory of energy losses in randomly heterogeneous medium
S. Panyukov, A. Leonidov
Theoretical Physics Department P.N. Lebedev Physics Institute, 119991 Moscow, Russia
Abstract
We derive equation describing distribution of energy losses of the particle propagating in fractal medium with quenched and dynamic heterogeneities. We show that in the case of the medium with fractal dimension 2<D<3 the losses Δ are characterized by the sublinear anomalous dependence 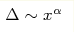 with power-law dependence on the distance
x from the surface and
exponent α=D-2. with power-law dependence on the distance
x from the surface and
exponent α=D-2.
|
 Home
Home