Home
For authors
Submission status

Archive
Archive (English)
Current
   Volumes 113-120
   Volumes 93-112
      Volume 112
      Volume 111
      Volume 110
      Volume 109
      Volume 108
      Volume 107
      Volume 106
      Volume 105
      Volume 104
      Volume 103
      Volume 102
      Volume 101
      Volume 100
      Volume 99
      Volume 98
      Volume 97
      Volume 96
      Volume 95
      Volume 94
      Volume 93
Search
VOLUME 98 (2013) | ISSUE 9 | PAGE 591
On the persistence of breathers at deep water
DOI: 10.7868/S0370274X13210029
Abstract
The long-time behavior of a perturbation to a uniform wavetrain of the compact Zakharov equation is studied near the modulational instability threshold. A multiple-scale analysis reveals that the perturbation evolves in accord with a focusing nonlinear Schrodinger equation for values of wave steepness 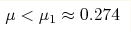\mu<\mu_{1}\approx0.274. The long-time dynamics is characterized by interacting breathers, homoclinic orbits to an unstable wavetrain. The associated Benjamin-Feir index is a decreasing function of μ, and it vanishes at μ1. Above this threshold, the perturbation dynamics is of defocusing type and breathers are suppressed. 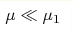Thus, homoclinic orbits persist only for small values of wave steepness \mu\ll\mu_{1}, in agreement with recent experimental and numerical observations of breathers.