
| VOLUME 98 (2013) | ISSUE 11 | PAGE 826 |
|---|
|
Extreme waves statistics for Ablowitz-Ladik system
D. S. Agafontsev
Shirshov Institute of Oceanology of the RAS, 117218 Moscow, Russia Novosibirsk State University, 630090 Novosibirsk, Russia
Abstract
We examine statistics of waves for the problem of modulation instability development in the framework of discrete integrable Ablowitz-Ladik (AL) system. Modulation instability depends on one free parameter h that has the meaning of the coupling between the nodes on the lattice. For strong coupling 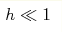 the probability density functions (PDFs) for waves amplitudes
coincide with that for the continuous classical Nonlinear Schrodinger (NLS)
equation; the PDFs for both systems are very close to Rayleigh ones. When the
coupling is weak the probability density functions (PDFs) for waves amplitudes
coincide with that for the continuous classical Nonlinear Schrodinger (NLS)
equation; the PDFs for both systems are very close to Rayleigh ones. When the
coupling is weak 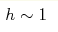 , there appear highly localized waves with very large
amplitudes, that drastically change the PDFs to significantly non-Rayleigh ones,
with so-called "fat tails" when the probability of a large wave occurrence is by
several orders of magnitude higher than that predicted by the linear theory.
Evolution of amplitudes for such rogue waves with time is similar to that
of the Peregrine solution for the classical NLS equation. , there appear highly localized waves with very large
amplitudes, that drastically change the PDFs to significantly non-Rayleigh ones,
with so-called "fat tails" when the probability of a large wave occurrence is by
several orders of magnitude higher than that predicted by the linear theory.
Evolution of amplitudes for such rogue waves with time is similar to that
of the Peregrine solution for the classical NLS equation.
|
 Home
Home