
| VOLUME 101 (2015) | ISSUE 9 | PAGE 709 |
|---|
|
Динамика спина в модели Френкеля с учетом изменения инерционных свойств электрона
С. Л. Лебедев
Сургутский государственный университет, 628412 Сургут, Россия
Abstract
В области значений параметров 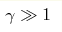 , ,
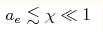 (γ - лоренц-фактор, (γ - лоренц-фактор,
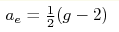 , ,
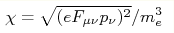 ) уравнения движения
модели Френкеля приводят к обобщению
системы уравнений Лоренца и Баргмана-Мишеля-Телегди (БМТ).
Модификация связана с учетом
френкелевской добавки mFr к массе электрона и может
представлять интерес для планируемых в настоящее время
экспериментов с релятивистскими пучками. Полученное
уравнение Френкеля-БМТ содержит продольную часть с зависящим
от времени коэффициентом, не равным нулю при g=2. В случае
постоянных фоновых полей уравнения траектории и спина могут быть
проинтегрированы с требуемой точностью, если известна
первообразная функции mFr(τ). Для спин-орбитального
вклада Δ mso в сдвиг массы найдено новое представление
через геометрические инварианты мировых линий. Показано, что
скорость изменения Δ mso определяется величиной ) уравнения движения
модели Френкеля приводят к обобщению
системы уравнений Лоренца и Баргмана-Мишеля-Телегди (БМТ).
Модификация связана с учетом
френкелевской добавки mFr к массе электрона и может
представлять интерес для планируемых в настоящее время
экспериментов с релятивистскими пучками. Полученное
уравнение Френкеля-БМТ содержит продольную часть с зависящим
от времени коэффициентом, не равным нулю при g=2. В случае
постоянных фоновых полей уравнения траектории и спина могут быть
проинтегрированы с требуемой точностью, если известна
первообразная функции mFr(τ). Для спин-орбитального
вклада Δ mso в сдвиг массы найдено новое представление
через геометрические инварианты мировых линий. Показано, что
скорость изменения Δ mso определяется величиной
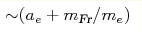 .
Указано на принципиальную возможность
периодического изменения спинового света вдоль траектории пучка. .
Указано на принципиальную возможность
периодического изменения спинового света вдоль траектории пучка.
|
 Home
Home