
| VOLUME 117 (2023) | ISSUE 7 | PAGE 556 |
|---|
|
Acoustic metric and Planck constants
G. E. Volovik
Low Temperature Laboratory, Aalto University, P.O. Box 15100, FI-00076 Aalto, Finland Landau Institute for Theoretical Physics, 142432 Chernogolovka, Russia
Abstract
Based on Akama-Diakonov (AD) theory of emergent tetrads, it was suggested that one can introduce two Planck constants, 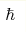 and \nh, which are the parameters of the corresponding
components
of Minkowski metric, gμν Mink = diag(-
\hbar2,\nh2,\nh2,\nh2). In the Akama-Diakonov theory, the interval ds is
dimensionless, as a result the metric elements and thus the Planck
constants have nonzero dimensions. The Planck constant and \nh, which are the parameters of the corresponding
components
of Minkowski metric, gμν Mink = diag(-
\hbar2,\nh2,\nh2,\nh2). In the Akama-Diakonov theory, the interval ds is
dimensionless, as a result the metric elements and thus the Planck
constants have nonzero dimensions. The Planck constant 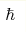 has
dimension of time, and the Planck constant \nh has dimension of length.
It is natural to compare \nh with the Planck length l P.
However, this connection remains an open question, because the
microscopic (trans-Planckian) physics of the quantum vacuum is not known.
Here we study this question using the effective gravity emerging for
sound wave quanta (phonons) in superfluid Bose liquid, where the
microscopic physics is known, and the elements of the effective acoustic
metric are determined by the parameters of the Bose liquid. Since the
acoustic interval is dimensionless, one may introduce the effective
"acoustic Planck constants". The acoustic Planck constant \nh ac
has dimension of length and is on the order of the interatomic distance.
This supports the scenario in which \nh \sim l P. We also use the
acoustic metric for consideration of dependence of has
dimension of time, and the Planck constant \nh has dimension of length.
It is natural to compare \nh with the Planck length l P.
However, this connection remains an open question, because the
microscopic (trans-Planckian) physics of the quantum vacuum is not known.
Here we study this question using the effective gravity emerging for
sound wave quanta (phonons) in superfluid Bose liquid, where the
microscopic physics is known, and the elements of the effective acoustic
metric are determined by the parameters of the Bose liquid. Since the
acoustic interval is dimensionless, one may introduce the effective
"acoustic Planck constants". The acoustic Planck constant \nh ac
has dimension of length and is on the order of the interatomic distance.
This supports the scenario in which \nh \sim l P. We also use the
acoustic metric for consideration of dependence of 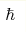 on the Hubble
parameter in expanding Universe. on the Hubble
parameter in expanding Universe.
|
 Home
Home