JETP Letters: issues online

We discuss the two-step transitions in superconductors, where the intermediate state between the Cooper pair state and the normal metal is the 4-fermion condensate, which is called the intertwined vestigial order. We discuss different types of the vestigial order, which are possible in the spin-triplet superfluid ³He, and the topological objects in the vestigial phases. Since in ³He the order parameter A_α i represents the analog of gravitational tetrads, we suggest that the vestigial states are possible in quantum gravity. As in superconductors, the fermionic vacuum can experience two consequent phase transitions. 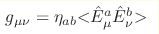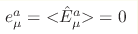At first transition the metric appears as the bilinear combination of tetrads $g_{\mu\nu} =\eta_{ab}{<} \hat E^a_\mu \hat E^b_\nu{>}$ , while the tetrad order parameter is still absent, $e_\mu^a={<} \hat E^a_\mu{>} =0$ . This corresponds to the bosonic Einstein general relativity, which emerges in the fermionic vacuum. 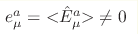The nonzero tetrads $e_\mu^a={<} \hat E^a_\mu{>} \neq 0$ appear at the second transition, where a kind of the Einstein-Cartan-Sciama-Kibble tetrad gravity is formed. This suggests that on the levels of particles, gravity acts with different strength on fermions and bosons.