
| VOLUME 117 (2023) | ISSUE 3 | PAGE 248 |
|---|
|
Dimensionless physics: Planck constant as an element of Minkowski metric
G. E. Volovik
Low Temperature Laboratory, Aalto University, P.O. Box 15100, FI-00076 Aalto, Finland Landau Institute for Theoretical Physics, 142432 Chernogolovka, Russia
Abstract
Diakonov theory of quantum gravity, in which tetrads emerge as the bilinear combinations of the fermionic fields, suggests that in general relativity the metric may have dimension 2, i.e. [gμν]=1/[L]2. Several other approaches to quantum gravity, including the model of superplastic vacuum and BF-theories of gravity support this suggesuion. The important consequence of such metric dimension is that all the diffeomorphism invariant quantities are dimensionless for any dimension of spacetime. These include the action S, interval s, cosmological constant Λ, scalar curvature R, scalar field Φ, etc. Here we are trying to further exploit the Diakonov idea, and consider the dimension of the Planck constant. The application of the Diakonov theory suggests that the Planck constant 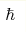 is the parameter of the
Minkowski metric.
The Minkowski parameter is the parameter of the
Minkowski metric.
The Minkowski parameter 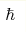 is invariant only under Lorentz
transformations, and is not diffeomorphism invariant. As a result the
Planck constant is invariant only under Lorentz
transformations, and is not diffeomorphism invariant. As a result the
Planck constant 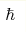 has nonzero dimension - the dimension of length
[L].
Whether this Planck constant length is related to the Planck length
scale, is an open question.
In principle there can be different Minkowski vacua with their own
values of the parameter has nonzero dimension - the dimension of length
[L].
Whether this Planck constant length is related to the Planck length
scale, is an open question.
In principle there can be different Minkowski vacua with their own
values of the parameter 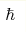 . Then in the thermal contact between the
two vacua their temperatures obey the analog of the Tolman law: . Then in the thermal contact between the
two vacua their temperatures obey the analog of the Tolman law:
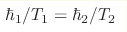 . .
|
 Home
Home