
| VOLUME 121 (2025) | ISSUE 10 | PAGE 806 |
|---|
|
First law of de Sitter thermodynamics
G. E. Volovik
Landau Institute for Theoretical Physics, 142432 Chernogolovka, Russia
Abstract
The de Sitter state has a special symmetry: it is homogeneous, and its curvature is constant in space. Since all the points in the de Sitter space are equivalent, this state is described by local thermodynamics. This state has the local temperature T=H/π (which is twice the Gibbons-Hawking temperature), the local entropy density, the local energy density, and also the local gravitational degrees of freedom - the scalar curvature 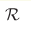 and the effective
gravitational coupling K. On the other hand, there is the cosmological
horizon, which can be also characterized by the thermodynamic relations.
We consider the connections between the local thermodynamics and the
thermodynamics of the cosmological horizon. In particular, there is the
holographic connection between the entropy density integrated over the
Hubble volume and the Gibbons-Hawking entropy of the horizon, S volume=S horizon=A/4G. We also consider the first law of
thermodynamics in these two approaches. In the local thermodynamics, on
the one hand, the first law is valid for an arbitrary volume V of de
Sitter space. On the other hand, the first law is also applicable to the
thermodynamics of the horizon. In both cases, the temperature is the
same. This consideration is extended to the contracting de Sitter with
its negative entropy, S volume=S horizon=-A/4G. and the effective
gravitational coupling K. On the other hand, there is the cosmological
horizon, which can be also characterized by the thermodynamic relations.
We consider the connections between the local thermodynamics and the
thermodynamics of the cosmological horizon. In particular, there is the
holographic connection between the entropy density integrated over the
Hubble volume and the Gibbons-Hawking entropy of the horizon, S volume=S horizon=A/4G. We also consider the first law of
thermodynamics in these two approaches. In the local thermodynamics, on
the one hand, the first law is valid for an arbitrary volume V of de
Sitter space. On the other hand, the first law is also applicable to the
thermodynamics of the horizon. In both cases, the temperature is the
same. This consideration is extended to the contracting de Sitter with
its negative entropy, S volume=S horizon=-A/4G.
|
 Home
Home