Дрюма В.С.

Институт Математики и Информатики АН Молдовы

valdryum@gmail.com

 Статья посвящена применению открытого в 1967 году метода обратной задачи теории рассеяния (ОЗТР)  для точного интегрирования нелинейного уравнения в ч.пр.,

\begin{equation} \left(U_t+UU_x+U_{xxx}\right)_x+\pm U_{yy}=0, \end{equation}

широко известного в настоящее время как уравнение Кадомцева-Певиашвили (КП) и которое описывает распространение слабо-дисперсионных волн в различных разделах физики плазмы и

гидродинамики. Автором впервые было установлено, что возможности метода ОЗТР могут быть существенно расширены и его можно с успехом применять  для точного интегрирования многомерных нелинейных дифференциальных \\уравнений, в том числе и имеющих физический интерес. Операторное представление Лэкса $\hat L_t=[\hat L,\hat A]$) для изучаемого уравнения, составляющее основу метода ОЗТР ранее было известно лишь для урвнения Кортевега-де Вриза ($U_t+UU_x+U_{xxx}=0$) и для нелинейного уравнения Шредингера (НШ) ($\Psi_t+\Psi_{xx}+|\Psi|^2\Psi=0$), позволило построить широкие классы точных решений для этих уравнений, что и привело в дальнейшем к отрытию нового понятия в нелинейной физике -солитона. В настоящее время многомерное обобщение метода ОЗТР используется для решения различного рода проблем диффференциальной и алгебраической геометрии, а также в задачах теории поля и гравитации. Открытие калибровочной эквивалентности между НШ-уравнением  $ iv_t+v_{xx}+2|v|^2v=0 $ и уравнением KП в теории "волн-убийц", встречающихся при изучении волн в океане и в задачах газовой динамики позволило установить важные закономерности их распространения, которые могут быть полезнвми для практических применений.

1. Б.Б.Кадомцев, В.И.Петвиашвили, ДАН СССР 192(4),(1970), 753-756.
2. В.С. Дрюма, ДАН  СССР, 268(1),(1983),15–17.
3. Новиков С.П.(ред.) Теория солитонов: метод обратной задачи, (Наука, 1980),  166 стр.
4. P. Dubard and V. B, Matveev, "Multi-rogue waves solutions: from the NLS to the KP-I equation", Nonlinearity, v. 26 (2013), R93–R125.

В.Э. Адлер, ИТФ им. Л.Д. Ландау

Статья посвящена приложениям следующего замечательного преобразования. Несложное вычисление показывает, что если $\psi(x,\lambda)$ общее решение уравнения

\[ \psi''=(u(x)-\lambda)\psi,\]

а $\psi_0(x)$ частное решение, отвечающее значению $\lambda=\lambda_0$, то

функция

\[ \tilde\psi=\psi'-w\psi,\quad w=\psi'_0/\psi_0\]

удовлетворяет уравнению того же вида, но с новым потенциалом $\tilde u=u-2w'$.Впервые это наблюдение было сделано в работе Дарбу [1], и впоследствии переоткрыто Шрёдингером [2,3] в контексте квантовой механики. Последовательность преобразований Дарбу описывается операторами $H_n=d^2/dx^2-u_n$, $Q^\pm_n=d/dx\pm w_n$, связанных соотношениями факторизации

\[ H_n+\lambda_n=Q^+_nQ^-_n \quad\mapsto\quad H_{n+1}+\lambda_n=Q^-_nQ^+_n, \]

что эквивалентно цепочке дифференциально-разностных уравнений

\[ u_n=w'_n+w^2_n+\lambda_n,\quad  w'_n+w'_{n+1}=w^2_n-w^2_{n+1}+\lambda_n-\lambda_{n+1}.\]

Любое решение этих уравнений порождает семейство операторов $H_n$ с $\psi$-функциями, явно вычисляемыми при всех $\lambda=\lambda_n$; операторы $Q^\pm_n$ играют роль операторов рождения-уничтожения. Как оказалось, практически все точно-решаемые модели квантовой механики (гармонический осциллятор, задача Кеплера, сферические гармоники, безотражательные потенциалы, потенциалы Морса, Пёшля--Теллера и т.д.) допускают единообразное описание в рамках этого метода [4,5]. При этом,

функции $w_n$, отвечающие разным $n$, имеют один и тот же вид и отличаются только значениями параметров.

Формулировка этого свойства {\em форм-инвариантности} и является основным результатом работы Генденштейна. В дальнейшем, эта идея получила развитие в работах Шабата, Веселова, Спиридонова [6-8] и др., в которых были введены новые семейства точно-решаемых потенциалов (в отличие от рассматривавшихся ранее, они выражаются не через элементарные функции, а через трансценденты Пенлеве и их обобщения).

Преобразование Дарбу допускает обобщение и для нестационарного уравнения Шрёдингера, и для других спектральных задач. Следует отметить его прямую связь с суперсимметрией [9-11] и с преобразованиями Бэклунда для нелинейных уравнений, интегрируемых методом обратной задачи рассеяния [12,13, 7]. Развитие этих теорий, происходившее в 1970--90 гг., шло параллельно и рассматриваемая статья оказала заметное влияние на эти исследования.

[1] G. Darboux. Sur une proposition relative aux ´equations lin´eaires. Compt. Rend. Acad. Sci. 94 (1882) 1456–1459. [arXiv:physics/9908003]
[2] E. Schr¨odinger. A method of determining quantum-mechanical eigenvalues and eigenfunctions. Proc. Roy. Irish Acad. A 46 (1940/1941) 9–16. [Перевод: Э. Шредингер, Избранные труды по квантовой механике, М.: Наука,  1976]
[3] E. Schrodinger. Further studies on solving eigenvalue problems by factorization. Proc. Roy. Irish Acad. A 46 (1940/1941) 183–206.
[4] L. Infeld, T.E. Hull. The factorization method. Rev. Modern Phys. 23:1 (1951) 21–68. [Перевод: "Математика"'  10:3 (1966) 39]
[5] M.M. Crum. Associated Sturm-Liouville systems. Quart. J. Math. Oxford Ser. 2 6 (1955) 121–127.
[6] A.B. Shabat. The infinite-dimensional dressing dynamical system. Inverse Problems 8 (1992) 303–308.
[7] А.П. Веселов, А.Б. Шабат.  Одевающая цепочка и спектральная теория оператора Шредингера.Функц. анализ 27:2 (1993) 1-21.
[8] V. Spiridonov. Exactly solvable potentials and quantum algebras. Phys. Rev. Lett. 69 (1992) 398–401.
[9] E. Witten. Dynamical breaking of supersymmetry. Nucl. Phys. B 188:3 (1981) 513–554.
[10]  Л.Э. Генденштейн, И.В. Криве.  Суперсимметрия в квантовой механике. Усп. физ. наук 146:4 (1985) 553–590.
[11]  В.Г. Багров, Б.Ф. Самсонов.  Преобразование Дарбу, факторизация, суперсимметрия в одномерной  квантовой механике. Теор. Мат. Физ. 104:2 (1995) 356–367.
[12] H.D. Wahlquist, F.B. Estabrook. B¨acklund transformations for solutions of the Korteweg–de Vries equation. Phys. Rev. Let. 31:23 (1973) 1386–1390.
[13] V.B. Matveev. Darboux transformation and explicit solutions of the Kadomtcev-Petviaschvily equation, depending on functional parameters. Lett. Math. Phys. 3:3 (1979) 213–216.
 

И. В. Полюбин

  ИТФ им. Л.Д. Ландау, ИТЭФ

В 1973 году появилась пионерская работа С. Коулмана и Э. Вайнберга [1] о влиянии квантовых  поправок на спонтанное нарушение калибровочной  симметрии.

 В настоящей работе автор изучает физические следствия учета этих однопетлевых поправок в эффективном потенциале скалярного поля. Рассмотрена модель комплексного скалярного поля с потенциалом $V=\lambda(\varphi^*\varphi)^2-{\mu}^2{\varphi}^*{\varphi}$, взаимодействующего  минимальным образом с электромагнитным полем с константой связи $g$. Условия  перенормировки для эффективного потенциала выбираются таким образом, чтобы вакуумное среднее $\sigma$ и масса скалярной частицы совпадали с классическими значениями. Эффективный потенциал имеет второй минимум при $<\varphi>=0$. Условие нарушения симметрии $V_{eff}(\sigma)< V_{eff}(0)$ накладывает ограничение на константу самодействия:

$$\lambda>\frac {3}{32{\pi}^2}g^4$$

Даже если затравочная (классическая) константа самодействия $\lambda$ сколь угодно мала, с учетом однопетлевых поправок ($\lambda\ll g^2$) $\lambda_{eff}=\lambda+\frac {1}{2{\pi}^2}g^4$. Так как масса скалярной частицы пропорциональна $\lambda$, а векторной $g$ из приведенных выше неравенств следует ограничение снизу на массу скалярной частицы. Для реалистических значений констант в работе получено ограничение на массу хиггсовой частицы: $m_H>5$ Гэв. На неабелев случай это ограничение было вскоре обобщено С. Вайнбергом [2]. С учетом вклада W, Z - бозонов, как самых тяжелых частиц, теоертически известных в то время, $m_H>7.4$Гэв. Это ограничение снизу на массу хиггсового бозона получило в литературе название - условие Линде-Вайнберга.

Следует отметить, что учет фермионов в петле при вычислении эффективног потенциала ослабляет условие Линде- Вайнберга [3]. Учет t-кварка делает эффективный потенциал неограниченным снизу, что означает неприменимость однопетлевого приближения. В двухпетлевом приближении [4,5] несимметричный вакуум становится близок к границе метастабильности при $m_H\simeq126$Гэв, $m_t\simeq174$Гэв [6].

[1] S. R. Coleman, E. J. Weinberg, Phys. Rev. D7 (1973), 1888-1910

[2] S. Weinberg, Phys.Rev.Lett. 36 (1976)294–296

[3]  Hung P. Q.  Phys. Rev. Lett. 42 (1979)873–876

[4] Casas J. A., Espinosa J. R., Quiros M. and Riotto A. 1995 Nucl. Phys. B436 (1995)3–29

[5] Hambye T. and Riesselmann K 1997 Phys. Rev. D55 (1997)7255–7262

[6] Isidori G., Ridolfi G. and Strumia A., Nucl. Phys. B609 (2001)387–409

В. А. Ходель
НИЦ "Курчатовский институт", Москва, 123182
McDonnell Center for the Space Sciences & Department of Physics, Washington University, St.~Louis, MO 63130, USA

В. Р. Шагинян

НИЦ "Курчатовский институт", Петербургский институт ядерной физики им. Б.П. Константинова, Гатчина, 188300

В статье, опубликованной более 25 лет назад, был введен новый тип фазового перехода и заложен фундамент теории сильно коррелированных ферми-систем, где теория Ландау перестает
работать[1]. Фазовый переход происходит, когда эффективная масса квазичастиц расходится, $M^*\to\infty$, а сами фермионы становится тяжелыми. За точкой перехода возникает
фермионный конденсат (ФК): энергия $\varepsilon(p)$ квазичастиц с импульсами $p_i<p<p_f$ равна химическому потенциалу $\mu$, и спектр становится плоским; здесь $p_i<p_F<p_f$ и $p_F$ является ферми-импульсом [1]. Главное отличие новой теории от стандартной заключалось в том, что в ней импульсное распределение квазичастиц $n(p)$ не совпадает с их
распределением в идеальном ферми-газе, а находится из вариационного условия $\delta E(n)/\delta n(p)=\mu$, что является естественным следствием идеи Ландау, что энергия $E$
ферми-системы является функционалом ее квазичастичного распределения $n(p)$. Исследования Г. Е. Воловика показали, что системы с ФК представляют новый класс ферми-жидкостей,
характеризуемый особым топологическим зарядом, что обеспечивает устойчивость этих систем по отношению к возмущениям [2-4]. Дальнейшие
исследования показали, что ФК появляется в 1D фермионах, захваченных в ядрах квантованных вихрей и возникающих, например, в сверхтекучем $\rm ^3He$, и ФК приводит к сверхпроводимости при комнатной температуре [3-4]. Свойства ФК были рассмотрены П. Нозьером: он привел соображения, что время жизни $\tau$ квазичастиц безнадежно мало, он же
показал, как следует изучать поведение ФК при конечных температурах $T$ [5] вместе с тем, дальнейшие исследования продемонстрировали, что $\tau\propto 1/T$, и квазичастицы хорошо определены [6, 7].

В результате, теория ФК позволила объяснить многочисленные экспериментальные данные, относящиеся к сильно коррелированным ферми-системам, представленными металлами с тяжелыми фермионами и высокотемпературными сверхпроводниками [4, 8, 9], спиновыми квантовыми жидкостями [10]] квазикристаллами [11] и двумерными ферми-системами [12, 13]. Сильно коррелированные ферми-системы ведут себя настолько необычно, что возникает необходимость пересмотреть многие разделы традиционной физики твердого тела и жидкостей. Есть
эффекты, отсутствующие в физике конденсированного состояния. Например, нарушение симметрии квазичастица-дырка, асимметрия в туннельной проводимости, обнаруженная в измерениях на металлах с тяжелыми фермионами, нарушение закона Видемана-Франца. Теория позволила выявить одинаковое скейлинговое поведение в различных сильно коррелированных ферми-системах и сделать вывод, что в этих системах реализуется новое состояние вещества. Таким образом в рамках теории ФК возникает неожиданно простое и одновременно хорошее описание сильно коррелированных ферми-систем [1-14].

[1] V. A. Khodel and V. R. Shaginyan, JETP Lett. 51, 553 (1990).
[2] G. E. Volovik, JETP Lett. 53, 222 (1991).
[3] G. E. Volovik, JETP Lett. 59, 830 (1994).
[4] G. E. Volovik, Phys. Scr. T 164, 014014 (2015).
[5] P. Nozieres, J. Phys. I France 2, 443 (1992).
[б] V. A. Khodel, V. R. Shaginyan, and P. Shuck, JETP Lett. 63, 752 (1996).
[7] J. W. Clark, V. A. Khodel, and M. V. Zverev, Phys. Rev. B 71, 012401 (2005).
[8] V. A. Khodel, V. R. Shaginyan, and V. V. Khodel, Phys. Rep. 249, 1 (1994).
[9] V. R. Shaginyan, M. Ya. Amusia, A. Z. Msezane, and K. G. Popov, Phys. Rep. 492, 31 (2010).
[10] V. R. Shaginyan, A. Z. Msezane, and K. G. Popov, Phys. Rev. B 84, 060401(R) (2011).
[11] V. R. Shaginyan, A. Z. Msezane, and K. G. Popov, G. S. Japaridze, and V. A. Khodel, Phys. Rev. B 87, 245122 (2013).
[12] V. R. Shaginyan, A. Z. Msezane, K. G. Popov, and V. A. Stephanovich, Phys. Rev. Lett. 100, 096406 (2008).
[13] A. A. Shashkin, V. T. Dolgopolov, J. W. Clark, V. R. Shaginyan, M.V. Zverev, and V. A. Khodel, Phys. Rev. Lett. 112, 186402 (2014).
[14] M. Ya. Amusia, K. G. Popov, V. R. Shaginyan, and V. A. Stephanovich, Theory of Heavy-Fermion Compounds - Theory of Strongly Correlated Fermi-Systems, Springer Series in Solid-State Sciences 182, (2014).

M.A. Shifman

School of Physics and Astronomy, University of Minnesota, Minneapolis, MN

55455, USA
 William I. Fine Theoretical Physics Institute, University of Minnesota,

Minneapolis, MN 55455, USA

            Пингвинный механизм, или пингвинная диаграмма, представляет собой класс диаграмм Фейнмана, имеющих огромное значение для понимания слабых распадов с изменением аромата. В то время как в оригинальной работе [1] рассматривались только распады частиц, содержащих странный кварк, сама идея была затем обобщена на широкий класс других приложений, например, на процессы с нарушением CP-чётности в распадах B мезонов, электрослабые пингвинные диаграммы и многие другие. (Сам термин “пингвинная диаграмма” был предложен Джоном Эллисом несколько позднее - см. ниже). Первые приложения данного механизма были опубликованы авторами в работе [2]. В B-физике “пингвины” чувствительны к новой физике, особенно это касается редких распадов, в которых пингвинные диаграммы доминируют. Такие распады были непосредственно измерены в 1991 и 1994 годах коллаборацией CLEO.

Пингвинный механизм в физике высоких энергий был обнаружен [1] в 1974 году. Это было самое начало эры квантовой хромодинамики (КХД). В 1973 году мы занялись изучением взаимного влияния сильных и слабых взаимодействий. Наиболее загадочным в распадах странных частиц казалось необъяснимое усиление амплитуд с ∆I = 1/2 в распадах каонов и барионов по сравнению с амплитудами с ∆I = 3/2. Загадка, известная как “правило ∆I = 1/2”, обсуждалась Дж. Швингером ещё в 1964 году. Появление КХД породило новые надежды на объяснение данного явления. Публикация [4] Гайар и Ли, дошедшая до ИТЭФ в виде препринта, послужила для нас стимулом. В частности, авторы заметили, что обмены  глюонами по- разному действуют в амплитудах с ∆I = 1/2 и с ∆I = 3/2: в первом случае они имеют тенденцию усиливать эффект, а во втором - ослаблять [5]. Тем не менее, одной этой тенденции было недостаточно для объяснения эффекта. Когда мы обнаружили пингвинные диаграммы и осознали, что их появление возможно лишь в части амплитуды распада странного кварка с ∆I = 1/2, мы поняли, что находимся на правильном пути. Специфические киральные свойства присущие только пингвинам привели в конечном итоге к успешному завершению вывода правила ∆I = 1/2 (см. обзор [3]). Летом 1974 года этот результат был доложен на международной конференции.

За четыре десятилетия, прошедших с момента появления пингвинных диаграмм, их развитие в приложении к различным процессам с изменением аромата было просто поразительным.  Публикуя свою работу в “Письмах в ЖЭТФ” мы, конечно же, не могли этого предположить.  В то время недавно открытые (SVZ) диаграммы ещё не выглядели похожими на пингвинов. Форму, напоминающую пингвина, им придал Джон Эллис.

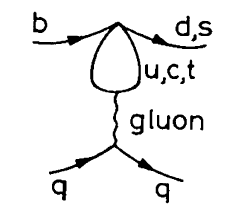
Диаграмма SVZ в “пингвинном” исполнении Джона Эллиса

Вот как выглядит история Джона, путешествующая теперь с одного вебсайта на другой (впервые она опубликована в [6]): “Мэри К. [Гайар], Димитрий [Нанопулос] и я впервые заинтересовались тем, что теперь называется пингвинными диаграммами, в процессе изучения нарушения CP инвариантности в стандартной модели в 1976. Название пингвин появилось в 1977 году следующим образом. Весной 1977 года Майк Чановиц, Мэри К. и я опубликовали статью, в которой из теории великого объединения предсказали массу b кварка до того, как он был найден. Сразу же после его обнаружения несколькими неделями позднее Мэри К., Димитрий, Серж Руда и я немедленно принялись за работу над его феноменологией. В то лето аспиранткой в ЦЕРН была Мелисса Франклин -- в настоящее время профессор Гарварда, экспериментатор. Как-то вечером она, Серж и я зашли в паб, и мы с ней стали играть в дротики. Мы договорились, что в случае проигрыша я должен буду в своей следующей статье использовать слово пингвин. Вообще говоря, она покинула игру ещё до её окончания, и за неё доигрывал Серж, который у меня выиграл. Тем не менее, я чувствовал себя обязанным выполнить условие пари.  В течение некоторого времени мне было неясно, каким образом можно включить слово пингвин в статью про b кварк, которую мы в тот момент писали. Затем однажды вечером, возвращаясь домой после работы в ЦЕРН, я заглянул к друзьям, жившим в Мейране, у которых я покурил какую-то травку. Позднее, когда я уже вернулся домой и продолжил работу над статьёй, меня внезапно осенило, что на пингвинов похожи известные диаграммы. Так мы ввели это имя в нашу работу, а остальное, как говорится, история.”

Литература

[1]  A.I. Vainshtein, V.I. Zakharov, M.A. Shifman, Pisma ZhETF 22, 123 (1975) [JETP Lett. 22, 55  (1975)].

[2] M. A. Shifman, A. I. Vainshtein and V. I. Zakharov, Nucl. Phys. B120  316 (1977) Non-leptonic decays of K-mesons and hyperons. ZhETF 72  1275  (1977) [JETP 45  670 (1977)].

[3] A. I. Vainshtein, Int. J. Mod. Phys. A 14, 4705 (1999) [hep-ph/9906263].

[4] M.K. Gaillard and B. Lee, Phys. Rev. Lett. 33, 108 (1974).

[5] Mary K. Gaillard, A Singularly Unfeminine Professions, (World Scientific, Singapore, 2015), p. 59.

[6] M. Shifman, ITEP Lectures in Particle Physics, (World Scientific, Singapore, 1999), Vol. 1, p. x [hep-ph/9510397].

M.A. Shifman

School of Physics and Astronomy, University of Minnesota, Minneapolis, MN

55455, USA
 William I. Fine Theoretical Physics Institute, University of Minnesota,

Minneapolis, MN 55455, USA

Работа [1] послужила основой так называемого метода правил сумм SVZ (иногда называемого методом правил сумм КХД), который позволяет вычислить параметры большого числа низколежащих адронных состояний исходя из средних характеристик КХД-вакуума, такие как кварковый и глюонный конденсаты (последний был введен в [1]). Основным концептуальным элементом этого метода является Вилсоновское операторное разложение (ОР). В исходной работе Вилсона основное внимание уделялось статистической физике, где Вилсоновская программа известна также под именем блок-спинового метода. Как это ни удивительно, в физике высоких энергий в начале и середине 1970х годов ОР понималось весьма узко и применялось по существу только в теории возмущений.  Авторы [1] и последующих публикаций [2] впервые применили развитый ими вариант Вилсоновского операторного разложения к квантовой хромодинамике. Их цель была такова: систематическое разложение по степенным поправкам на малых расстояниях (т.е. по конденсатам локальных операторов), с последующей экстраполяцией на большие расстояния. Для этой экстраполяции и сшивки с адронами использовались дисперсионные соотношения (после борелевского улучшения).

Эта идея не потеряла значимости и сегодня. Применения метода SVZ были многочисленными и успешными. Он был проверен в работе — при вычислении практически всех статических характеристик всех низколежащих адронных состояний, как мезонных так и барионных — и всюду он доказал свою продуктивность (см. обзор [3]). Позднее, уже в 1980-ые и 90-ые годы, метод SVZ был развит и обобщен для применений в разложениях по тяжелому кварку, которые широко использовались для точных предсказаний для b-содержащих мезонов и барионов  в 1990х годах в связи потоком новых экспериментальных данных (см. обзор [4]). 

Вопрос, который мы задали сами себе в 1977 г. и который вскоре привел нас к идее вакуумных конденсатов параметризующих свойства адронов, был таков (см. также  [5]:

 - Что если начать с малых расстояний, на которых кварк-глюонная динамика описывается теорий возмущений, и перейти к большим расстояниям, а после этого произвести сшивку с адронным представлением, используя общие свойства КХД…

Как это ни странно, первые интересные результаты для чармония стали получаться почти сразу, а чуть позднее, когда в коллаборацию влились В. Новиков, Л. Окунь и М. Волошин успеx превзошел все ожидания. Вшестером мы показали, основные параметры  большого количества  связанных состояний  cc могут быть (и были) надежно предсказаны. Здесь стоит упомянуть один эпизод. Согласно тогдашним экспериментальным данным единственным кандидатом на роль псевдоскалярного чармония был Х(2.83). Его масса казалось слишком низкой для этой интерпретации; тем не менее ее все же удавалось “втиснуть”  в тогда популярные потенциальные модели. В работе [6] было показано, что правила сумм КХД не допускают столь большого расщепления между 1^- и  0⁺ состояниями.

Иными словами,  Х(2.83) не мог быть  псевдоскалярным чармонием; масса , была предсказана в интервале 3,01± 0,01 GeV. Позднее экспериментальные данные о  Х(2.83) были дезавуированы. Нынешние данныe для массы этой частицы дают 2,983±  0,0007  GeV.

На протяжении примерно года мы продолжали извлекать массы и константы связи cc частиц из рациональных отношений плюс небольшие поправки. Ранним летом 1977 года был написан обзор [7], через несколько месяцев он был отправлен в редакцию. Примерно в это же время стало ясно, что наш успех носил ограниченный характер: он не обобщался на обычные мезоны и барионы, построенные из легких кварков.

Стояло жаркое лето, как раз перед отпуском. Наша большая коллаборация распалась. Но обсуждение продолжалось, в неспешном темпе. Тут-то как раз и возникла идея, что вакуум КХД похож на глюонную среду и свойства частиц определяются кварковый взаимодействием с этой средой, которое может быть параметризовано некоторыми кварковыми и глюонными конденсатами. Первое приложение глюонного конденсата было опробовано в r мезоне. Сначала нам показалось, что ничего не получается  поскольку один знак в ключевой формуле был не тем,  как хотелось бы. Однако вскоре мы поняли что четырехкварковый конденсат компенсирует этот знак, и это было началом прорыва.

Точность предсказаний оказалась намного лучше, чем можно было бы ожидать априори.

Вдохновленные этим, мы лихорадочно работали весь академический год. Когда окончательная статья вышла в Nuclear Physics (маленькая заметка появилась еще раньше, в самом начале,  в Письмах ЖЭТФ) она заняла целый номер, около 300 страниц. Препринт было сделать невозможно, поскольку согласно тогдашним бюрократическим правилам препринт не мог содержать больше одного “печатного листа”. Поэтому мы разбили статью на семь или восемь отдельных препринтов, постаравшись сделать это таким образом, чтобы цензорам это вопиющее нарушение правил было не заметно.

Литература:

[1]  A.I. Vainshtein, V.I. Zakharov and M.A. Shifman, Pis'ma ZhETF 27 , 60 (1978) [JETP Lett. 27, 55 (1978)] .

[2] M. A. Shifman, A. I. Vainshtein and V. I. Zakharov, Nucl. Phys. B 147, 385 (1979), and Nucl. Phys. B 147, 448 (1979).

[3] M. A. Shifman, Prog. Theor. Phys. Suppl. 131,  1 (1998)  [hepph/9802214].

[4] I. I. Y. Bigi, M. A. Shifman and N. Uraltsev, Ann. Rev. Nucl. Part. Sci. 47, 591 (1997) [hep-ph/9703290].

[5] M. Shifman, Current Contents,  32, 9 (1992).

[6] V. A. Novikov et al., Phys. Rept. 41, 1 (1978).