In recent years, there has been great interest in the intense plasma flows generated by plasma focus facilities, which are widely used in various fields. In particular, laboratory experiments on modeling astrophysical jets developed, for which plasma focus facilities also proved to be in demand [1].
However, there has not been an unambiguous point of view on the mechanisms of flow launch until now. The most popular mechanisms were cumulative plasma outflow either at the stage of compression of the plasma current sheath (PCS) to the axis, or during the development of constrictions already on the body of the formed pinch [2, 3]. The paper presents experimental data and a theoretical model that make it possible to formulate a fundamentally new look on the physics of the launching mechanism of plasma ejection in a plasma focus discharge.

Experimental studies of the stage of the plasma jet generation at the ISPF-M plasma focus facility at the Kurchatov Institute have shown that the source of the plasma outflow propagating along the axis of the discharge system is a local region inside the PCS in its upper part. It shows that the plasma bunch moves in a well-defined direction upward from the anode, rather than in symmetrical directions, which would be expected, for example, when plasma flows out of a pinch constriction. A characteristic feature of this region is the presence of a radial component of the electric current, which leads to the appearance of a vertical component of the plasma velocity due to Ampère force. Already at the initial stages of the plasma bunch movement, it has a supersonic character, which leads to the formation of a shock wave. In this case, the upper boundary of the PCS is destroyed, which can lead to the reconnection of magnetic field lines and currents and the formation of a compact plasma bunch with a trapped magnetic flux propagating along the axis of the system, in accordance with the model formulated in [4].

The shadowgram of the discharge in argon at the second harmonic of the Nd:YAG laser (532 nm) 40 ns after the peak of the derivative of the discharge current corresponding to the phase of maximum pinch compression (a) and the shadowgram of the discharge in hydrogen at the fundamental harmonic (1064 nm) 29 ns (b) and 62 ns (c) after the peak of the derivative.

1. V.S. Beskin, V.I. Krauz, S.A. Lamzin, Physics – Uspekhi 66, 327 (2023).
2. N.V. Filippov, et al., Applied Physics (Prikladnaya Fizika) 5, 43 (1999).
3. S. N. Polukhin, at al. Plasma Physics Reports 46, 127 (2020).
4. K.N. Mitrofanov et al. JETP 119, 2010 (2014)

V. Krauz, V.  Beskin, M. Medvedev,  A. Kharrasov, V. Myalton
JETP Letters 122, issue 10 (2025)
 

High-luminosity collider NICA operation for study of the gluon contribution to the nucleon spin will require very high intensity of the primary polarized proton and deuteron beams out of the source. A new technique is proposed for the polarized source upgrade as an important step to achieve designed NICA luminosity. It is based on the effect of the target thickness increase with transverse injection of the polarized atomic beam into the storage cell of the charge-exchange plasma ionizer. The atomic beam ionization is produced in charge-exchange collisions of atomic beam with ions in plasma jet. The atomic beam in the existing source is injected into the ionizer cell in longitudinal direction and produced beam is extracted in the backward direction [1,2]. Transverse injection of the atomic beam into the storage cell will eliminate a number of limitations inherent to the longitudinal injection configuration and deliver the beam intensity and polarization out of the source to obtain the high luminosity in the NICA collider.

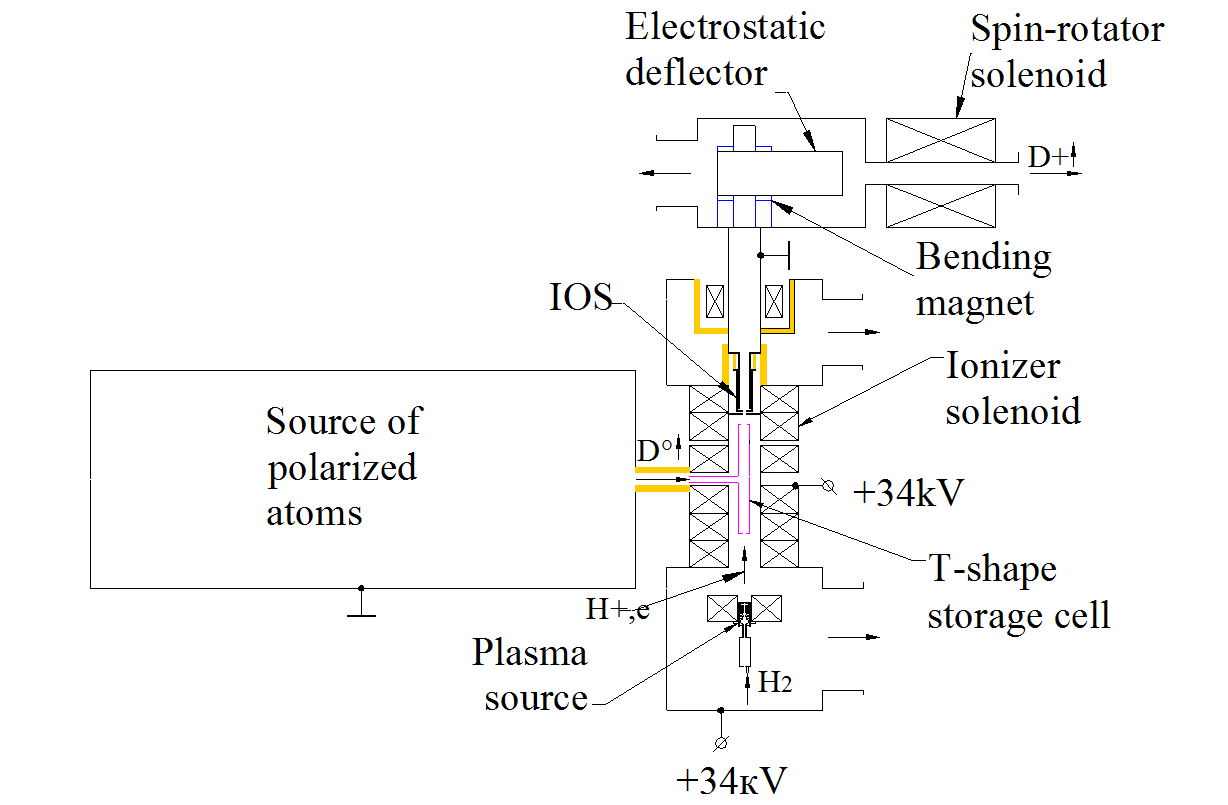
Schematic layout of a polarized source with transverse injection of atomic beam into the T-shape storage cell.

In this scheme, a polarized atomic beam is injected into the storage cell perpendicularly to the direction of the plasma jet and the magnetic field axis of the ionizer solenoid. The plasma is generated in an arc discharge generator with a cold cathode and injected into the storage cell along the magnetic field axis. Polarized ions produced in the storage cell are held in the radial direction by a magnetic field and move to the electrode of the ion-optical system, in which polarized and non-polarized ions from the plasma are accelerated. The distance between the source of polarized atoms and the entrance to the storage cell in this scheme is significantly reduced compared to longitudinal injection, since the bending magnet and the ion extraction electrode system are not in the path of the atomic beam. The diameter of the emission electrode in this scheme is determined by the diameter of the plasma jet and can be reduced, resulting in a corresponding decrease in emittance of the beam. The energy of the extracted ions can be increased.  since the size of the bending magnet and of the ion-optical system  do not affect the atomic beam intensity. All these factors combined should produce about ten-fold increase of the beam quality factor:  QF= I·P²/Ԑ², where I -is the beam intensity, P- polarization, Ԑ – transverse emittance- to meet NICA luminosity design goal.

[1] A.S. Belov, D.E. Donets, V.V. Fimushkin, A.D. Kovalenko, L.V. Kutuzova, Yu.V. Prokofichev, V.B. Shutov, A.V. Turbabin and V.N. Zubets,  J. Phys..: Conf. Ser. 938, 012017 (2017). doi:10.1088/17426596/938/1/012017

[2] A.S. Belov, AIP Conf. Proc. 980, 209 (2008).  doi:10.1063/1.2888089

A.C. Belov, A.N. Zelenski, K.A. Ivshin, M.V. Kulikov, V.A. Lebedev, A.N. Solov'ev, E.M. Suresin, Yu.N. Filatov, V.V. Fimushkin
JETP Letters 122, issue 8 (2025)

According to the conventional definition the Fermi surface in momentum space surrounds the positions of occupied particle states at zero temperature. This definition has the clear meaning  for the system of noninteracting Fermi-particles in the absence of inhomogeneities. 

In the presence of interactions the Fermi surface may be defined as the position of the poles of the Green function in momentum space. This definition is more general but it still cannot be applied in the presence of disorder or other sources of inhomogeneities. Then instead of the Green's function depending on momentum we can consider the Wigner transformed Green's function depending both on momentum and on coordinates. Its singularities in momentum space (or singularities of certain quantities composed of it) may   be considered as the space dependent Fermi surface. 
In the homogeneous systems the topological invariant responsible for the stability of the Fermi surface (or Fermi point) is composed of the one-particle Green function $G(p)$. It has the form of an integral along the three – dimensional hypersurface embracing the Fermi surface/Fermi point in momentum space. This expression may be extended to the case of the inhomogeneous systems. Then the form of the given expression is similar to that of the homogeneous system. There the Green's function $G(p)$ should be replaced by the Wigner transformed Green's function $G_W(p,x)$, and the ordinary products are to be replaced by the Moyal products $\star$. The integration over the coordinate space is to be added, while integration in momentum space should be performed along the hypersurface surrounding the positions of Fermi surfaces. Unlike the case of homogeneous system, in general case of the inhomogeneous system we cannot restrict integration to the compact hypersurface. It may have the form of the two hyperplanes of opposite orientations with constant Matsubara frequency $p_4= ±\epsilon$  ($\epsilon \to 0$, it is supposed that the Fermi surfaces are situated between these two hyperplanes):
\begin{eqnarray}
    {\cal N}&&
    =  {-} \frac{\epsilon_{ijk4}}{ |{\bf V}| \,3!\,4\pi^2}\, \int d^3x \int  d^3p
    \, {\rm tr}\, \hat{T} {G}_{W}(x,p )\nonumber\\&&\star \frac{\partial {Q}_{W}(x,p )}{\partial p_i} \star \frac{\partial  {G}_{W}(x,p )}{\partial p_j} \star \frac{\partial  {Q}_{W}(x,p )}{\partial p_k}
    \label{calM2d230I}
\end{eqnarray}
By $Q_W$ we denote the Weyl symbol of Dirac operator that is a solution of equation $Q_W  \star G_W=1$. Here $\bf V$  is the volume of the given system,  $\hat T$ is a symmetry matrix that commutes with both $Q_W$ and $G_W$. The above expression may also be rewritten in the form of an integral over infinite hypersurface $\Sigma$ embracing the Fermi surface that appears as deformation of the two hyperplanes mentioned above. 

There are certain questions concerning the above defined quantity. First of all, for the Dirac fermions with $\hat{T} = \gamma^5$  it enters expression for the conductivity of the chiral separation effect. Next, if the system may be continuously deformed to the uniform one, this topological invariant is reduced to the previously known quantity composed of the one-particle Green's function $G(p)$. In this case the nontrivial value of $\cal N$  is obtained due to the matrix structure of the Green's function and reveals analogy with the degree of mapping. An important question is whether exist the systems, in which the nontrivial value of $\cal N$  is not due to the matrix structure, but due to the spatial dependence of $G_W (p,x)$. We give examples of such systems in the present paper. Besides, there are certain (still unsolved) pure mathematical questions concerning the above mentioned expression of $\cal N$ itself. We are trying to address some of these questions as well. 

It is worth mentioning that the present paper does not represent the exhaustive description of all issues related to the given topological invariant. These issues still await their investigation. 


 

M. Zubkov
JETP Letters 122, issue 8 (2025)

Fractional quantum Hall effect states at total Landau level filling factors $\nu=\nu_{\rm Q}=8/3$, 7/3, 4/3, and 5/4 were investigated in a bilayer electron system created in a wide (60 nm) GaAs quantum well placed between two field electrodes (gates). It was found that these fractional states appear or greatly enhance when a magnetic field is tilted from the normal to the plane of the electron system and integer quantum Hall effect states at $\nu=\nu_{\rm Q}=1$ and 2 become essentially weaker or even disappear. Using a new experimental technique consisting of simultaneous measurements of the magnetoresistance and Hall resistance, as well as two capacitances between the gates and the electron system [1, 2], we have established that these fractions arise under conditions when an incompressible state is realized in the layer with a higher electron density at filling factors in this layer $\nu_{\rm TL}$ equal to 2 and 1. This observation allows the interpretation of fractional states at filling factors $\nu_{\rm Q}=8/3$, 7/3, and 4/3 as combinations of incompressible states of the integer quantum Hall effect in one layer and the fractional quantum Hall effect in the other layer (8/3=2+2/3, 7/3=2+1/3, 4/3=1+1/3). The state of the fractional quantum Hall effect at a total filling factor of 5/4 with an even denominator cannot be interpreted in this way [3] and indicates the existence of unexplored effects of interlayer electron correlation when incompressible state at a filling factor of unity exists in one of the layers. It has been established that incompressible states at $\nu_{\rm TL}=2$ and 1 are broadened in the magnetic field due to the redistribution of electrons between the layers, as a result of which, within one such state, two different fractional quantum Hall effect states can be observed (states at total filling factors $\nu_{\rm Q}=7/3$ and 8/3 in the figure).

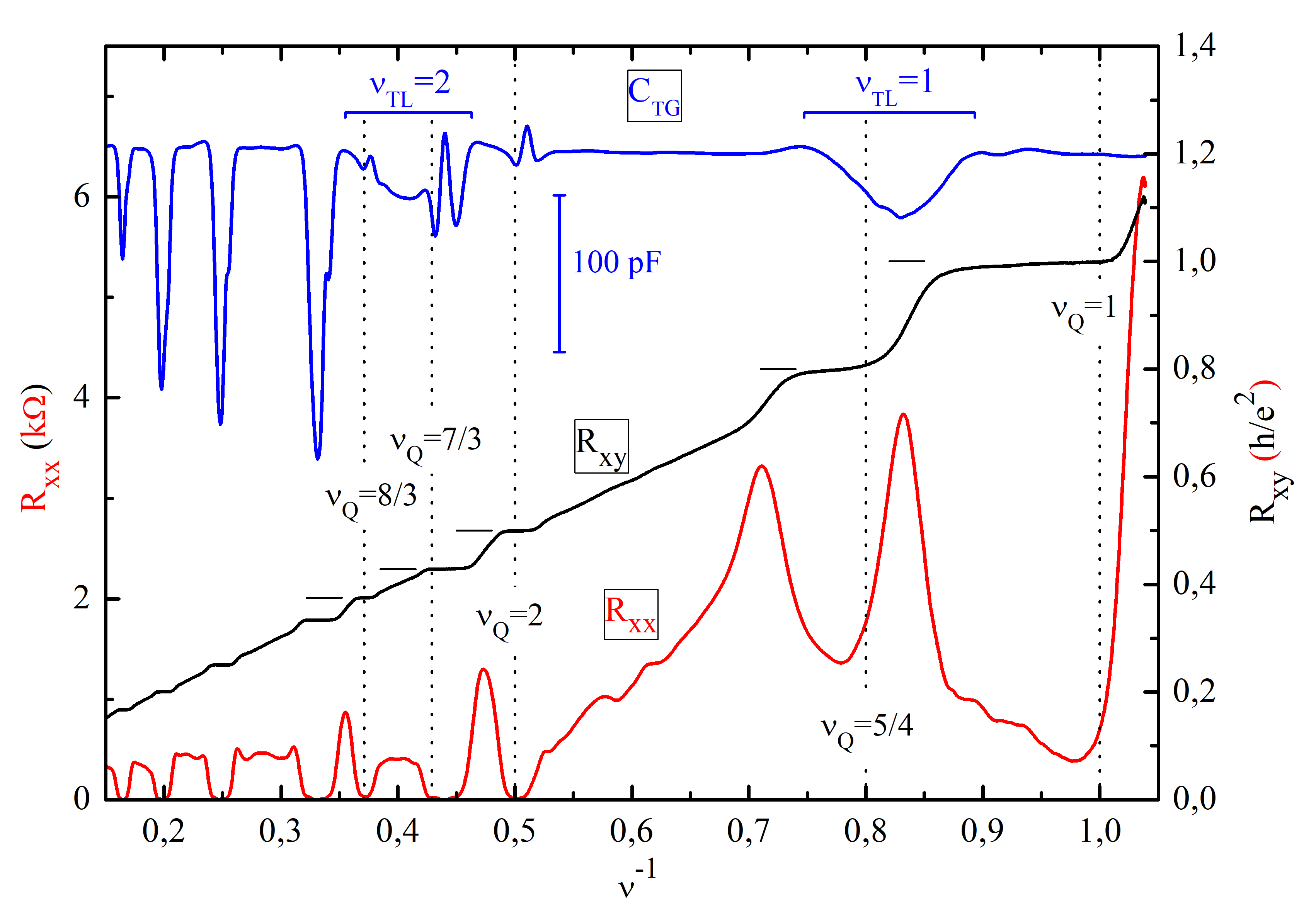
The magnetoresistance $R_{\rm xx}$, Hall resistance $R_{\rm xy}$, and magnetocapacitance $C_{\rm TG}$ between the top gate and the electron system versus inverse value $\nu^{-1}$ of the total filling factor $\nu$, which is proportional to the magnetic field component perpendicular to the system. The vertical dashed lines mark the expected positions $\nu_{\rm Q}$ of several quantum Hall effect states. The values of the quantum plateaus $R_{\rm xy}=\nu_{\rm Q}^{-1}h/e^2$ for these states are shown by the horizontal segments. The horizontal brackets mark the broad magnetocapacitance minima corresponding to incompressible states in the top electron layer at filling factors $\nu_{\rm TL}=2$ and 1. The tilt angle is equal to $45^{\circ}$, temperature $T=45$~mK.

1. S. I. Dorozhkin, A. A. Kapustin, I. B. Fedorov, V. Umansky, K. von Klitzing, and J.H. Smet, J. Appl. Phys. 123, 084301 (2018)
       2. S. I. Dorozhkin, A. A. Kapustin, I. B. Fedorov, V. Umansky, and J.H. Smet, Phys. Rev. B 102, 235307 (2020)
       3. S. I. Dorozhkin, A. A. Kapustin, I. B. Fedorov, V. Umansky, and J.H. Smet, JETP Lett. 117, 68 (2023)

S. I. Dorozhkin, A. A. Kapustin,  and J.H. Smet
JETP Letters 122, issue 7 (2025)

The superfluidity of 3He is associated with Cooper pairing of particles with a total orbital angular momentum and spin equal to 1. This allows the existence of superfluid phases with different structures and properties. However, in pure 3He in the absence of magnetic field, only the A and B phases are realized. When 3He is placed in a magnetic field, another phase, the so-called A1 phase, becomes accessible. The region of existence of the A1 phase is linear with respect to the field. Another method for the creation of new phases is the controlled introduction of impurities, which can be achieved by highly porous aerogels. Aerogel is a material consisting of solid strands whose size is much smaller than the distance between them.

When experiments are conducted in pure 3He in nematic aerogel, a pure A phase (instead of the polar phase which is favorable when the aerogel strands are covered with ~3 atomic layers of 4He) is realized with the superfluid transition temperature being noticeably suppressed [1]. Nematic aerogel consists of strands nearly parallel to one another. In pure 3He in aerogel, the transition temperature should also split in magnetic field, but the splitting is expected to be nonlinear at fields below the spin saturation field (~2 T) due to the influence of magnetic scattering [2].

Various resonators, such as a vibrating wire, can be used to study superfluid 3He. Its resonance parameters are determined by the properties of both the wire and the surrounding medium. In experiments with 3He, an aerogel sample is glued to such a vibrating wire. Liquid 3He fills the space between the aerogel strands, causing the resonance parameters to also depend on the properties of the liquid within the aerogel.

In the case of an anisotropic aerogel sample, in addition to the main mechanical resonance of the vibrating wire, a second oscillation mode is also observed. This mode is analogous to the second sound and arises from mutual oscillations of both the normal and superfluid components within the aerogel sample. In the series of experiments, scanning over a wider frequency range allowed us to measure the temperature dependences of the parameters of both resonance modes. Using the data, we were able to study the temperature dependence of the upper transition Tca1 over a wide range of magnetic fields, and we also managed to detect the lower transition Tca2 (from the A1 to the A2 phase) using high magnetic fields up to 3 T, which was not the case at fields <2 T [3].

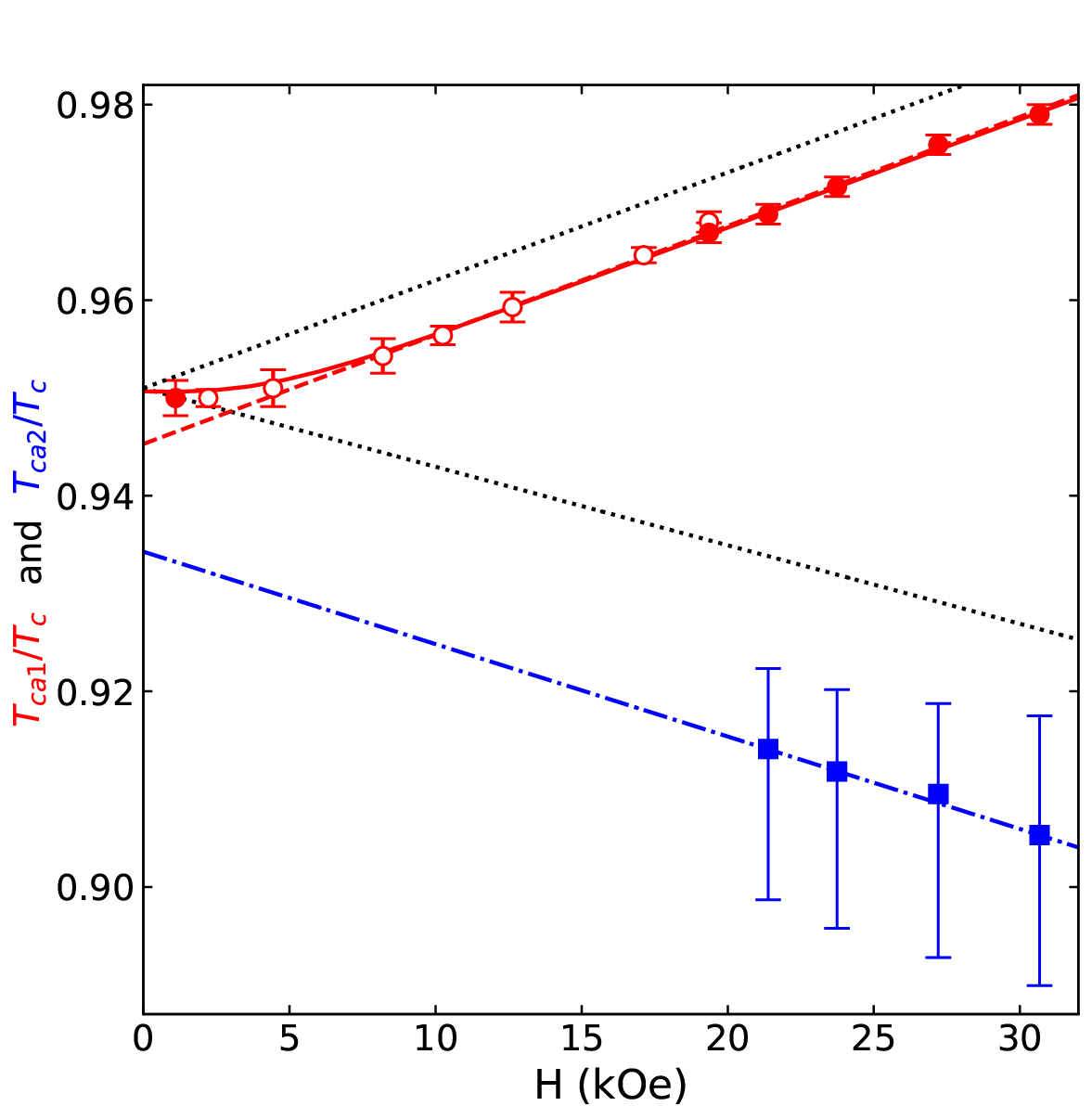
The A1–A2 splitting in pure 3He in nematic aerogel in magnetic field. The circles correspond to Tca1 (open circles are from [3]), the squares correspond to Tca2. The solid line is the best fit with theoretical model of [2], the dashed line is a linear extrapolation of the high-field Tca1 data to a zero field, and the dash-dotted line is a linear fit of the Tca2 data. Dotted lines correspond to the A1–A2 splitting in bulk 3He scaled to a superfluid transition temperature of 0.95Tc, where the superfluid transition temperature in bulk 3He Tc = 2.083 mK.

[1] V.V. Dmitriev, A.A. Soldatov, and A.N. Yudin, Phys. Rev. Lett. 120, 075301 (2018).

[2] G.A. Baramidze and G.A. Kharadze, J. Low Temp. Phys. 135, 399 (2004).

[3] V.V. Dmitriev, M.S. Kutuzov, A.A. Soldatov, and A.N. Yudin, Phys. Rev. B 107, 024507 (2023).

V. V. Dmitriev, M. S. Kutuzov, D. V. Petrova, A. A. Soldatov, A. N. Yudin,
JETP Letters 122, issue 7 (2025)

One prominent phenomenon in relativistic nucleus-nucleus collisions is jet quenching due to medium-induced partonic energy loss. The observable most directly associated with jet quenching is the suppression of the yield of hadrons with a high transverse momentum p_T, which is quantified by the nuclear modification factor, R_AA (p_T, η). It is defined as the ratio of the inclusive single-hadron yield per unit pseudorapidity η in AA collisions to the corresponding yield in pp collisions, scaled by the average number of binary nucleon-nucleon collisions. In this paper, we investigate the double nuclear modification factor, which was introduced in [1], to simultaneously probe initial and final state effects. We consider a more general case where both hard particles experience energy loss. The hypothesis of the factorization of this factor

R_AA (p_T1, η₁; p_T2, η₂) = F∙R_AA (p_T1,η₁)∙R_AA (p_T2,η₂)

is tested for different types of final-state hadrons within the framework of the HYDJET++ model.

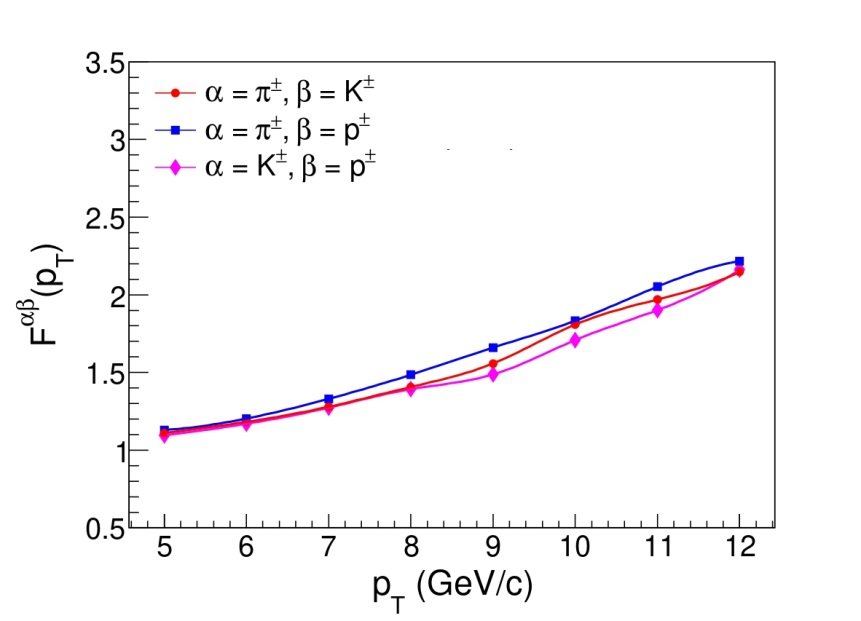
Fig.1 The dependence of the ratio F of the double and the product of single nuclear modification factors on the minimum value of the hadron transverse momentum p_T .

The deviation F from factorization of the production pions in association with kaons and (anti-)protons as well as the production of kaons in association with (anti-)protons was calculated for central PbPb collisions at center-of-mass energy 5.02 TeV per nucleon pair (Fig. 1). Results indicate that the hypothesis of factorization holds reasonably well at moderately high p_T, provided that the effects of double parton scattering can be small or neglected. However factorization violation starts to show at very high p_T. This supports the conclusion that measurements of the double nuclear modification factors offer significant potential for further investigations.

[1] S.P. Baranov, A.V. Lipatov, M.A. Malyshev, and A.M. Snigirev, JETP Letters 119, 823 (2024)

A. S.Chernyshov, I.P. Lokhtin, A.M. Snigirev
JETP Letters 122, issue 5 (2025)

At present, the generally a epted and widely used prop erty of multiparti le amplitudes is the absen e of simultaneous dis ontinuities of amplitudes in energy invariants of overlapping hannels. To justify this prop erty, the Steinmann relations are used. The pap er shows the presen e of su h dis ontinuities and the illegitima y of using the  teinmann relations to prove their absen e. In the ase of infrared singular parts of the amplitudes, the existen e of the simultaneous dis ontinuities is ompletely natural. But it is not limited to su h parts, and is not limited to the existen e of infrared singularities at all, but o urs also in their absen e. The pap er demonstrates the existen e of simultaneous dis ontinuities in the $s_{12}$ and $s_{23}$ hannels for the amplitude with three parti les in the nal state shown in the gure.

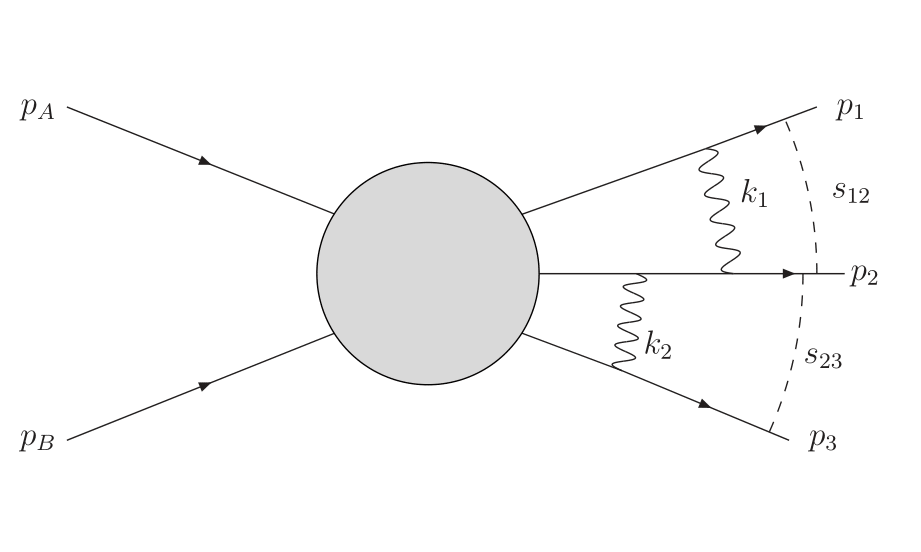
The existen e of simultaneous dis ontinuities means that the urrently a epted form of multi-Regge amplitudes is in orre t and should b e taken into a ount when deriving the BFKL (Balitsky-Fadin-Kuraev-Lipatov) equation in the higher approximations.

V. Fadin
JETP Letters 122, issue 4  (2025)

Contrary to their name, black holes in fact glow. According to Stephen Hawking’s famous result, black holes radiate energy and have a temperature. But where does this temperature come from?

In our research, we show that this strange heat of spacetime has a surprisingly topological origin. That is, it depends not just on the local properties of gravity, but on the global shape of spacetime itself. The Big Idea: Curvature Meets Topology.Every object-whether a donut or a sphere-has a property called the Euler characteristic. It's a number that tells you something deep about the object's shape. For example: A sphere has Euler characteristic 2, A donut (torus) has Euler characteristic 0. Our breakthrough is this: the temperature of spacetime horizons (like those around black holes or inside an expanding universe) is related to their Euler characteristic. We prove this using a powerful mathematical tool: the Chern-Gauss-Bonnet theorem, which links curvature and topology. But to apply it to spacetimes, we have to use a clever trick called Wick rotation--a way of turning time imaginary to smooth out the geometry. 


Black holes are examples of phenomena known as causal horizons - which are boundaries in spacetime across which events cannot influence each other due to the finite speed of light. These occur across many various spacetimes, and comprise an interesting intersection between gravity, quantum field theory, and thermodynamics. In the case of the Schwarzschild and de Sitter spacetimes, we find this connection can be characterised by the well-known Wick rotation (also known as analytic continuation) where $t \to i\tau$ and the resulting periodicity becomes $\tau \sim \tau + 2\pi \beta$. This periodicity in the Euclidean time $\tau$ is an indication of a non-trivial thermal state present within the spacetime - with temperature $T_H = 1/\beta$ - indicating a uniform radiation flux from the horizon. 

By applying the Wick rotation to these two well-studied phenomena:

1. 1. Schwarzschild Black Hole: A simple, non-rotating black hole. Its Euclidean version looks like a disc (D²) crossed with a sphere (S²). Its Euler characteristic is 2, and we show that the Hawking temperature is directly related to this number. 
2.  2. de Sitter Universe: A model of a universe filled with dark energy. Here too, Wick rotation gives us a compact space, and again the Euler characteristic determines the temperature-in this case, the Gibbons-Hawking temperature. 

This argument from Wick rotation places primary emphasis on the thermal properties of fields within spacetime. However, the analytic continuation $t \to i\tau$  and resulting angular compactification in $\tau$ is a non-trivial geometric operation that enforces global constraints on the topology of the manifold. For instance, in the case of de Sitter, this procedure maps the non-compact hyperbolic spacetime to the compact 4-sphere. The consequences of this from the geometric perspective are considerable: various integrals over scalars formed from the Riemann curvature are now guaranteed to converge (while before Wick rotation they automatically diverged in time $t$) to topological integers.

Fig.1 Under Wick rotation de Sitter space is transformed into an $S^4$ sphere  while  Black hole - into the product of disk and 2D sphere: $D^2\times S^2$. Both have Euler characteristic $\chi=2$}

Here we demonstrate that these considerations lead to a natural topological origin for horizon thermodynamics. For both Schwarzschild and de Sitter spacetimes, the temperature of the spacetime horizon is shown to be inversely proportional to the Euler characteristic $\chi$ (a topological integer) of the manifold after the Wick rotation and Euclidean time periodicity are performed. In addition, for de Sitter this framework explains topologically the origin of the discrepancy between the two physical temperatures discussed extensively by G. Volovik, A. Polyakov and others. Therefore, while the thermal field theory perspective is computationally powerful in quantifying horizon dynamics, the latter is in fact the consequence of a duality between the causal structure of a spacetime and the global topology of its analytical continuation. 

So why does it matter? This topological approach gives us: 

•  A unified framework to understand horizon temperatures.
•   A new geometrical insight into why time becomes periodic near a horizon.
•   A profound link between heat and shape-suggesting that spacetime itself may know its temperature because of its topology. 

In short, we show that temperature is not just about energy-it's about the shape of space itself.

Hughes J.C.M. and Kusmartsev F.V. 
JETP Letters 122, issue 4 (2025)

 

This work presents the results of direct numerical simulation of gravity water wave turbulence within a fully nonlinear plane-symmetric model. We show that in 1D geometry, the spectrum of weak turbulence of plane gravity waves generated by five-wave resonant interactions (suggested in [1]) is not realized. Instead of that, the main contribution to turbulence is due to wave breaking, which produces a power-law spectrum in both the frequency range and the wavenumber space with the same exponent equal to −4, see Fig.1. To our knowledge, our results represent the first direct numerical confirmation of the strong turbulence spectra predicted in [2]. In strongly nonlinear regime, the calculated probability density function (PDF) for the surface gradient has power-law tails with exponents close to −7/2, which indicates intermittency in turbulence.

Fig.1. The calculated frequency and spatial spectra of surface perturbations compared to the power-law dependencies ω^-4 and k^-4.

1. A.I. Dyachenko, Y.V. Lvov, V.E. Zakharov, Physica D 87(1-4), 233(1995)

2. E.A.Kuznetsov, JETP Lett. 80(2) ,83 (2004)

E.  Kochurin and E. Kuznetsov
JETP Letters 122, issue 4 (2025)

The work proposes an analytical theory of nonlinear generation of large-scale magnetic turbulence in collisionless plasma with an anisotropic velocity distribution of particle in the presence of an external magnetic field. Based on the results of the dispersion analysis of the Weibel-type instability in magnetoactive collisional plasma, and with use of the quasilinear approach, a system of equations describing the evolution of the mean-square magnetic-field energy density of small- and large-scale components of the turbulent field is obtained.

It is shown that, even in the absence of interparticle collisions, anomalous collisions of particles due to scattering on small-scale magnetic fluctuations lead to instability of long-wave harmonics, which are stable in the linear approximation. The non-linear growth of such harmonics at a given anisotropy of the particle velocity distribution, consistent with the dynamics of short-wave perturbations at the saturation stage and possible anisotropic particle injection, occurs in the superexponential regime and corresponds to an explosive-type instability (Fig. 1).

The growth law of the large-scale magnetic field is found analytically and the critical time of explosive instability is estimated. This type of fundamental plasma process is expected in a number of transient phenomena in laboratory and astrophysics, e.g., in accretion disks and jets, in stellar winds and coronal flares, in collisionless shock waves and laser ablation processes.

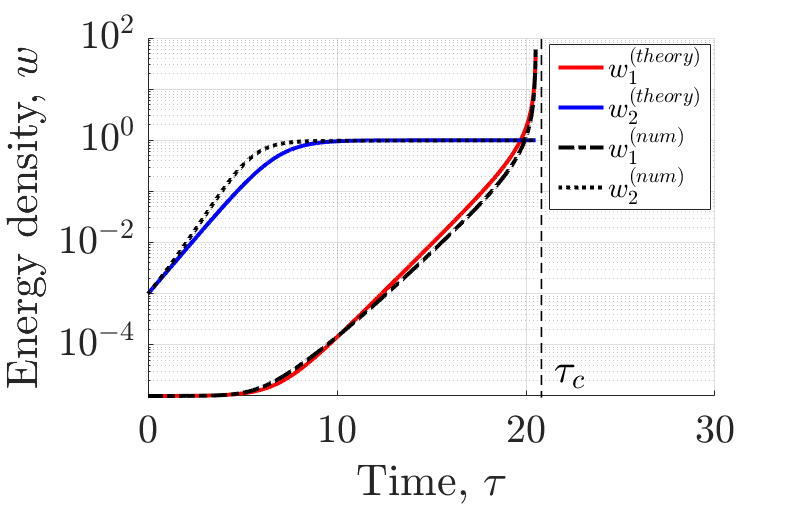
Fig.1 Time dependence of the mean-square magnetic-field energy density $w$. The dotted and dash-dotted lines are numerical solutions for small- and large-scale components of the turbulent field, and the blue and red solid lines are analytical solutions, respectively. A formal explosion takes place at a normalized time $\tau_c$.

N.Emel’yanov and V.V.Kocharovskii
JETP Letters 122, issue 2 (2025)